题目内容
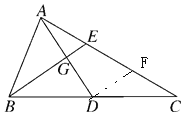
【题目】如图，AD，BE分别是△ABC的中线和角平分线，AD⊥BE于点G，AD＝BE＝6，求AC的长．
【答案】 
【解析】试题分析：过D点作DF∥BE，交AC于点F.根据平行线分线段的性质，可得DF的长，然后根据勾股定理求出AF的长，再根据三角形的中位线的性质和等腰三角形的性质和判定求解即可.
试题解析：过D点作DF∥BE，交AC于点F.
∵AD是△ABC的中线，AD⊥BE
∴F为CE的中点，AD⊥DF.
∴DF是△BCE的中位线，∠ADF＝90°.
∵AD＝BE＝6，
∴DF＝
BE＝3
∴AF＝
＝3
.
∵BE是△ABC的角平分线
∴∠ABG＝∠DBG.
∵AD⊥BE
∴AG＝DG，
即G为AD的中点．
∵BE∥DF，
∴E为AF的中点
∴AE＝EF＝CF＝
AF
∴AC＝
AF＝
×3
＝
.
练习册系列答案
教材全解字词句篇系列答案
相关题目
【题目】在一次“构造勾股数”的探究性学习中，老师给出了下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中
、
为正整数，且
．
（
）观察表格，当
， 
时，此时对应的
、
、
的值能否为直角三角形三边的长？说明你的理由．
（
）探究
， 
， 
与
、
之间的关系并用含
、
的代数式表示： 
__________， 
__________， 
__________．
（
）以
， 
， 
为边长的三角形是否一定为直角三角形？如果是，请说明理由；如果不是，请举出反例．
