题目内容
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为cm.
【答案】24﹣8 ![]()
【解析】解:如图所示,建立直角坐标系,过A作AG⊥OC于G,交BD于Q,过M作MP⊥AG于P,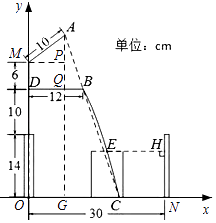
由题可得,AQ=12,PQ=MD=6,故AP=6,AG=36,
∴Rt△APM中,MP=8,故DQ=8=OG,
∴BQ=12﹣8=4,
由BQ∥CG可得,△ABQ∽△ACG,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴CG=12,OC=12+8=20,
∴C(20,0),
又∵水流所在抛物线经过点D(0,24)和B(12,24),
∴可设抛物线为y=ax2+bx+24,
把C(20,0),B(12,24)代入抛物线,可得![]() ,解得
,解得 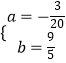 ,
,
∴抛物线为y=﹣ ![]() x2+
x2+ ![]() x+24,
x+24,
又∵点E的纵坐标为10.2,
∴令y=10.2,则10.2=﹣ ![]() x2+
x2+ ![]() x+24,
x+24,
解得x1=6+8 ![]() ,x2=6﹣8
,x2=6﹣8 ![]() (舍去),
(舍去),
∴点E的横坐标为6+8 ![]() ,
,
又∵ON=30,
∴EH=30﹣(6+8 ![]() )=24﹣8
)=24﹣8 ![]() .
.
所以答案是:24﹣8 ![]() .
.

【题目】学校为了丰富学生课余活动开展了一次“校园歌手大奖赛”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70,9.60
B.9.60,9.60
C.9.60,9.70
D.9.65,9.60
【题目】在一次“构造勾股数”的探究性学习中,老师给出了下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中![]() 、
、![]() 为正整数,且
为正整数,且![]() .
.
(![]() )观察表格,当
)观察表格,当![]() ,
, ![]() 时,此时对应的
时,此时对应的![]() 、
、![]() 、
、![]() 的值能否为直角三角形三边的长?说明你的理由.
的值能否为直角三角形三边的长?说明你的理由.
(![]() )探究
)探究![]() ,
, ![]() ,
, ![]() 与
与![]() 、
、![]() 之间的关系并用含
之间的关系并用含![]() 、
、![]() 的代数式表示:
的代数式表示: ![]() __________,
__________, ![]() __________,
__________, ![]() __________.
__________.
(![]() )以
)以![]() ,
, ![]() ,
, ![]() 为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.