题目内容
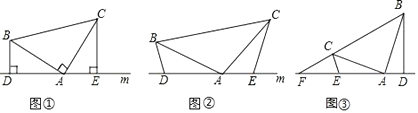
【题目】(1)如图①,在△ABC中,∠BAC=90,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.E证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D. A.E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请问结论DE=BD+CE是否成立,若成立,请你给证明:若不存在,请说明理由。
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,D. A.E三点都在直线m上,且∠BDA=∠AEC=∠BAC,只出现m与BC的延长线交于点F,若BD=5,DE=7,EF=2CE,求△ABD与△ABF的面积之比。
【答案】(1)见解析;(2)成立,理由见解析;(3)2:9
【解析】
(1)证明△ABD≌△CAE,根据全等三角形的性质证明即可;
(2)根据三角形内角和定理证明∠CAE=∠ABD,证明△ABD≌△CAE,根据全等三角形的性质证明即可;
(3)根据(2)的结论求出AE、AD、EF,根据三角形的面积公式计算即可.
(1)证明:∵∠BAC=90°
∴∠BAD+∠CAE=90°
∵CE⊥直线m
∴∠ACE+∠CAE=90°
∴∠BAD=∠ACE
在△ABD和△CAE中
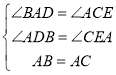
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE
∴DE=AE+AD=BD+CE
(2)结论DE=BD+CE成立
证明:∠CAE=180°﹣∠BAC﹣∠BAD,
∠ABD=180°﹣∠ADB﹣∠BAD,
∴∠CAE=∠ABD
在△ABD和△CAE中
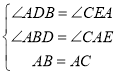
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE
∴DE= AE+ AD =BD+CE
(3)由(2)得,△ABD≌△CAE
∴AE=BD=5,
∴AD=DE﹣AE=2
∴EF=2CE=4
∴△ABD与△ABF的面积之比=AD:AF=2:9




