Question

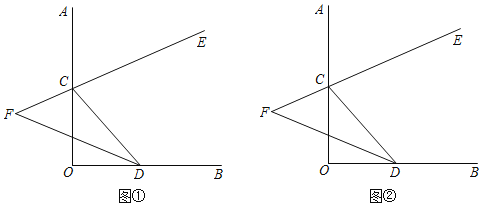
【题目】如图，在平面直角坐标系中，点，以为直径在第一象限内作半圆，为半圆上一点，连接并延长至，使，过作轴于点，交线段于点，已知，抛物线经过、、三点．

________°．

求抛物线的函数表达式．

若为抛物线上位于第一象限内的一个动点，以、、、为顶点的四边形面积记作，则取何值时，相应的点有且只有个？

Answer 1

【答案】(1)90;(2);(3) 以P、O、A、E为顶点的四边形面积S等于16时，相应的点P有且只有3个．

【解析】

（1）利用圆周角定理，直径所对的圆周角等于90°，即可得出答案；
（2）利用（1）中的结论易得OB是AC的垂直平分线，易得点B，点C的坐标，由点O，点B的坐标易得OB所在直线的解析式，从而得出点E的坐标，用待定系数法得抛物线的解析式；
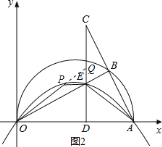
（3）利用（2）的结论易得点P的坐标，分类讨论①若点P在CD的左侧，延长OP交CD于Q，如右图2，易得OP所在直线的函数关系式，表示出Q点的纵坐标，
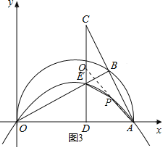
得QE的长，表示出四边形POAE的面积；②若点P在CD的右侧，延长AP交CD于Q，如右图3，易得AP所在直线的解析式，从而求得Q点的纵坐标，得QE求得四边形POAE的面积，当P在CD右侧时，四边形POAE的面积最大值为16，此时点P的位置就一个，令，解得p，得出结论．

解：(1)；连接，如图所示，
∵由知，又，
∴是的垂直平分线，
∴，
在中，，，
∴，
∴，
∴所在直线的函数关系为，
又∵点的横坐标为，
∴点纵坐标为，

即，
抛物线过，，，
∴设此抛物线的函数关系式为，把点坐标代入得：
，
解得．
∴此抛物线的函数关系式为，即；

设点，
①若点在的左侧，延长交于，如右图，
所在直线函数关系式为：
∴当时，，即点纵坐标为，
∴，

，
，

②若点在的右侧，延长交于，如右图，

，
∴设所在直线方程为：，把和坐标代入得，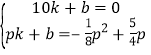
，
解得．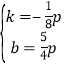
∴所在直线方程为：，
∴当时，，即点纵坐标为，
∴，
∴



，
∴当在右侧时，四边形的面积最大值为，此时点的位置就一个，
令，解得，，
∴当在左侧时，四边形的面积等于的对应的位置有两个，
综上所知，以、、、为顶点的四边形面积等于时，相应的点有且只有个．