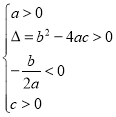题目内容
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
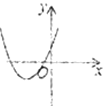
方程有两个不相等的负实根 |
|
|
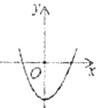
____________ |
|
|
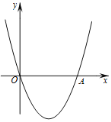
方程有两个不相等的正实根 | ____________ | ____________ |
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(1)由二次函数与一元二次方程的关系以及二次函数与系数的关系容易得出答案;
(2)根据题意得出关于m的不等式组,解不等式组即可.
解:(1)表格如下:

故答案为:方程有一个负实根,一个正实根;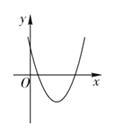 ;
; .
.
(2)设一元二次方程![]() 对应的二次函数为:
对应的二次函数为:![]() ,
,
∵一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,
有一个负实根,一个正实根,且负实根大于-1,
∴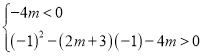 ,解得:
,解得:![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
【题目】函数图象y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
x | 。。。 | -1 | 0 | 1 | 2 | 3 | 4 | 。。。 |
y | 。。。 | 10 | 5 | 2 | 1 | 2 | 5 | 。。。 |
(1)求二次函数解析式 ;
(2)若![]() ,
,![]() 两点都在该函数图像上,且
两点都在该函数图像上,且![]() ,则
,则![]() 与
与![]() 的大小关系
的大小关系
(第一问写过程,第二问直接写结果)