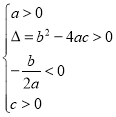题目内容
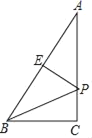
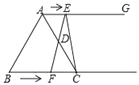
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s)
(1)填空:当t为 s时,△ABF是直角三角形;
(2)连接EF,当EF经过AC边的中点D时,四边形AFCE是否是特殊四边形?请证明你的结论.
【答案】(1)2或8;(2)四边形AFCE是平行四边形,证明见解析;
【解析】
(1)△ABF中,由△ABC是等边三角形可知∠B=60°≠90°,所以∠BAF与∠AFB可以等于90°,需分类讨论.画出图形,利用特殊三角函数值求出BF的长,除以点F速度即求得t的值.
(2)由AG∥BC可得∠EAD=∠FCD,∠AED=∠CFD,再加上点D为AC中点易证△ADE≌△CDF,进而得DE=DF,根据对角线互相平分的四边形为平行四边形可得四边形AFCE为平行四边形.再求此时AE、CF的长,说明∠AFC不等于90°和AF≠AE,排除四边形AFCE是菱形或矩形.
解:(1)∵等边△ABC中,BC=8cm
∴∠ABC=60°≠90°,AB=BC=8cm
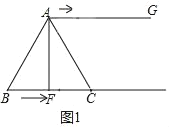
①如图1,若∠AFB=90°,则∠BAF=30°
∴BF=![]() AB=4cm
AB=4cm
∴t=BF÷2=2(s)
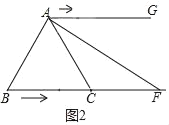
②如图2,若∠BAF=90°,则∠AFB=30°
∴BF=2AB=16cm
∴t=BF÷2=8(s)
故答案为:2或8.
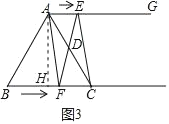
(2)四边形AFCE是平行四边形,证明如下:
如图3,过点A作AH⊥BC于点H
∵∠ABC=60°,AB=8cm
∴sin∠ABC=![]() ,cos∠ABC=
,cos∠ABC=![]()
∴AH=![]() AB=4
AB=4![]() cm,BH=
cm,BH=![]() AB=4cm
AB=4cm
∵AG∥BC
∴∠EAD=∠FCD,∠AED=∠CFD
∵点D是AC中点
∴AD=CD
在△ADE与△CDF中
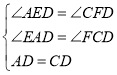
∴△ADE≌△CDF(AAS)
∴DE=DF
∴四边形AFCE是平行四边形
∴AE=CF
∵AE=t,CF=BC﹣BF=8﹣2t
∴t=8﹣2t
解得:t=![]()
∴AE=![]() cm,BF=
cm,BF=![]() cm
cm
∴BF>BH,AF>AH,∠AFC>90°
∴AF≠AE
∴四边形AFCE不是菱形或矩形,四边形AFCE是平行四边形.

【题目】某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
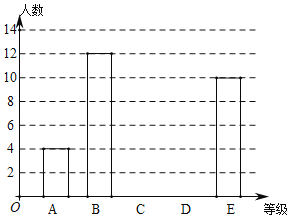
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“![]() 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
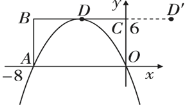
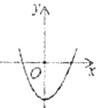
方程有两个不相等的负实根 |
|
|
____________ |
|
|
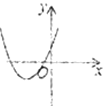
方程有两个不相等的正实根 | ____________ | ____________ |
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.