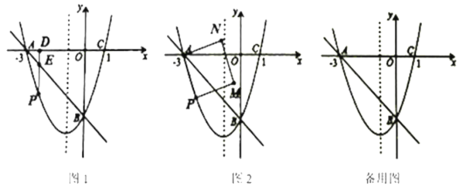
题目内容
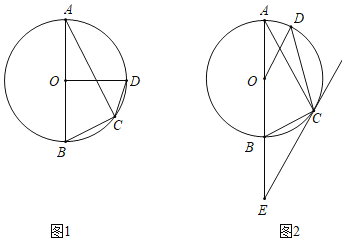
【题目】如图1,抛物线y = ax2+bx-3经过A、B、C三点，己知点A(-3,0)、C (1, 0).
（1）求此抛物线的解析式.
（2）点P是直线AB下方的抛物线上一动点(不与A、B重合)，
①过点F作x轴的垂线，垂足为D,交直线AB于点E,动点P在什么位置时，PE最大,求 出此时P点的坐标.
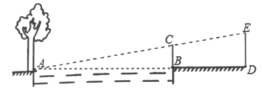
②如图2,连接AP.以AP为边作图示一侧的正方形APMN,当它恰好有一个顶点落在抛物 线对称轴上时，求出对应的P点的坐标.
【答案】（1）y = x2+2x﹣3；（2）①（﹣
，
），②（﹣
－1，2）或（
，
）
【解析】
（1）直接用待定系数法求解即可；
（2）①由抛物线解析式y = x2+2x﹣3，令x=0，y=﹣3，求出点B（0，-3），设直线AB的解析式为y=kx+b，把A（﹣3,0）和B（0，﹣3）代入y =kx+b求出k=-1，b=-3，直线AB的解析式为y=﹣x﹣3，设E（x，﹣x﹣3），则PE=﹣（x+）2+
，从而得当PE最大时，P点坐标为（﹣，）；
②抛物线对称轴为直线x=﹣1，A（﹣3,0），正方形APMN的顶点落在抛物线对称轴上的情况有两种情况，i) 当点N在抛物线对称轴直线x=﹣1上；ii）当点M在抛物线对称轴直线x=﹣1；根据这两种情况，作出图形，找到线段之间的等量关系，解之即可．.
（1）把A（﹣3,0）和C（1,0）代入y = ax2+bx﹣3得，
，解得
，
∴抛物线解析式为y = x2+2x﹣3；
（2）设P（x，x2+2x﹣3），直线AB的解析式为y=kx+b，
①由抛物线解析式y = x2+2x﹣3，令x=0，y=﹣3，
∴B（0，﹣3），
把A（﹣3,0）和B（0，﹣3）代入y =kx+b得，
解得
，
∴直线AB的解析式为y=﹣x﹣3，
∵PE⊥x轴，
∴E（x，﹣x﹣3），
∵P在直线AB下方，
∴PE=﹣x﹣3﹣（ x2+2x﹣3）=﹣x2﹣3x=﹣（x+）2+，
当x=﹣时，y= x2+2x﹣3=，
∴当PE最大时，P点坐标为（﹣，）.
②抛物线对称轴为直线x=﹣1，A（﹣3,0），正方形APMN的顶点落在抛物线对称轴上的情况有两种：
i)当点N在抛物线对称轴直线x=﹣1上时，作PR⊥x轴于点R，设对称轴与x轴的交点为L，如图①，
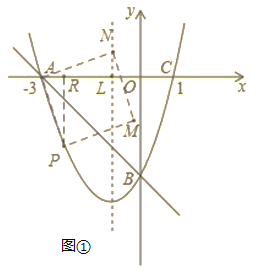
∵四边形APMN为正方形，
∴AN=AP，∠PAR+∠RAN=90°，
∵∠PAR+∠APR=90°，
∴∠APR=∠RAN，
在△APR和△NAL中
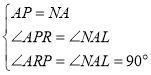
∴△APR≌△NAL（AAS），
∴PR=AL，
∵AL=﹣1－（﹣3）=2，
∴PR=2，此时 x2+2x﹣3=2，解得x1=－1，x2=﹣－1，
∵P在直线AB下方，
∴x=﹣－1，
∴P（﹣－1，2）；
ii)当点M在抛物线对称轴直线x=﹣1上时，如图②，过点P作PH⊥对称轴于点H、作AG⊥HP于点G，
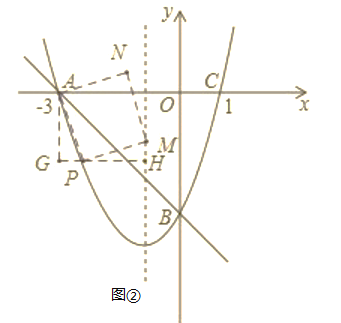
∵四边形APMN为正方形，
∴PA=PM，∠APM=90°，
∴∠APG+∠MPH=90°，
∵∠APG+∠GAP=90°，
∴∠GAP=∠HPM，
在△APG和△PMH中
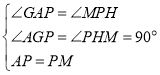
∴△APG≌△PMH（AAS），
∴AG=PH，PG=MH，
∴GH=PG+PH
∵P(x，x2+2x-3)
∴x+3+（-x2-2x+3）=2，解得x1=
，x2=，
∵P在直线AB下方，
∴x=，
∴P（，）
终上所述，点P对应的坐标为（﹣－1，2）或（，）.
