题目内容
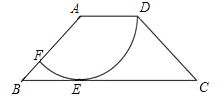
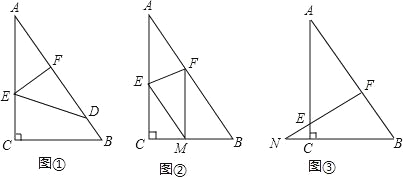
【题目】我们不妨约定：如图①，若点D在△ABC的边AB上，且满足∠ACD=∠B（或∠BCD=∠A），则称满足这样条件的点为△ABC边AB上的“理想点”．
（1）如图①，若点D是△ABC的边AB的中点，AC=
，AB=4.试判断点D是不是△ABC边AB上的“理想点”，并说明理由．
（2）如图②，在⊙O中，AB为直径，且AB=5，AC=4.若点D是△ABC边AB上的“理想点”，求CD的长．
（3）如图③，已知平面直角坐标系中，点A(0,2),B(0,-3),C为x轴正半轴上一点，且满足∠ACB=45°，在y轴上是否存在一点D，使点A是B，C，D三点围成的三角形的“理想点”，若存在，请求出点D的坐标；若不存在，请说明理由．
【答案】（1）是，理由见解析；（2）
；（3）D（0,42）或D（0,6）
【解析】
（1）依据边长AC=
，AB=4，D是边AB的中点，得到AC2=
，可得到两个三角形相似，从而得到∠ACD=∠B；
(2)由点D是△ABC的“理想点”，得到∠ACD=∠B或∠BCD=∠A，分两种情况证明均得到CD⊥AB，再根据面积法求出CD的长；
(3)使点A是B，C，D三点围成的三角形的“理想点”，应分两种情况讨论，利用三角形相似分别求出点D的坐标即可.
（1）D是△ABC边AB上的“理想点”，理由：
∵AB=4，点D是△ABC的边AB的中点，
∴AD=2，
∵AC2=8，
，
∴AC2=，
又∵∠A=∠A，
∴△ADC∽△ACB，
∴∠ACD=∠B，
∴D是△ABC边AB上的“理想点”.
（2）如图②，
∵点D是△ABC的“理想点”，
∴∠ACD=∠B或∠BCD=∠A,
当∠ACD=∠B时，
∵∠ACD+∠BCD=90
，
∴∠BCD+∠B=90，
∴∠CDB=90，
当∠BCD=∠A时，同理可得CD⊥AB，
在Rt△ABC中，∵∠ACB=90,AB=5，AC=4，
∴BC=
=3，
∵
,
∴
,
∴
.
（3）如图③，存在.
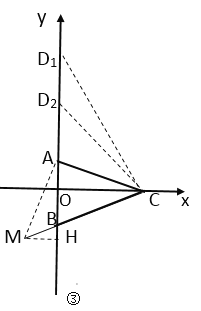
过点A作MA⊥AC交CB的延长线于点M，∵∠MAC=∠AOC=90,∠ACM=45，
∴∠AMC=∠ACM=45，
∴AM=AC,
∵∠MAH+∠CAO=90,∠CAO+∠ACO=90,
∴∠MAH=∠ACO,
∴△AHM≌△COA
∴MH=OA,OC=AH,
设C（a，0），
∵A(0，2),B(0，-3),
∴OA=MH=2，OB=3，AB=5，OC=AH=a，BH=a-5，
∵MH∥OC,
∴
，
∴
，
解得a=6或a=-1（舍去），
经检验a=6是原分式方程的解，
∴C（6,0），OC=6.
①当∠D1CA=∠ABC时，点A是△BCD1的“理想点”，
设D1(0，m)，
∵∠D1CA=∠ABC,∠CD1A=∠CD1B,
∴△D1AC∽△D1CB,
∴
,
∴
，
解得m=42，∴D1(0，42)；
②当∠BCA=∠CD2B时，点A是△BCD2“理想点”，
可知：∠CD2O=45，
∴OD2=OC=6，
∴D2（0,6）.
综上，满足条件的点D的坐标为D（0,42）或D（0,6）.
