题目内容
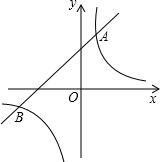
如图,正方形ABCD边长为2,AB∥x轴,AD∥y轴,顶点A恰好落在双曲线y=
上,边CD、BC分别交双曲线于点E、F,若线段AE过原点,则△AEF的面积为( )

| 1 |
| 2x |
| A.1 | B.
| C.
| D.
|

∵线段AE过原点,
∴点A、E关于坐标原点对称,
∵正方形ABCD的边长为2,
∴点A的纵坐标为-1,
代入反比例函数解析式得,
=-1,
解得x=-
,
∴点A(-
,-1),E(
,1),
∴点F的横坐标为2-
=
,
代入反比例函数解析式得y=
=
,
∴点F(
,
),
∴DE=
+
=1,EC=2-1=1,CF=1-
=
,FB=1+
=
,
△AEF的面积=22-
×2×1-
×1×
-
×2×
=4-1-
-
=
.
故选D.
∴点A、E关于坐标原点对称,
∵正方形ABCD的边长为2,
∴点A的纵坐标为-1,
代入反比例函数解析式得,
| 1 |
| 2x |
解得x=-
| 1 |
| 2 |
∴点A(-
| 1 |
| 2 |
| 1 |
| 2 |
∴点F的横坐标为2-
| 1 |
| 2 |
| 3 |
| 2 |
代入反比例函数解析式得y=
| 1 | ||
2×
|
| 1 |
| 3 |
∴点F(
| 3 |
| 2 |
| 1 |
| 3 |
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
△AEF的面积=22-
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
故选D.

练习册系列答案
相关题目