Question

【题目】如图，Rt△ABC中，∠C=90°，∠A=30°，点D，E分别在边AC，AB上，点D与点A，点C都不重合，点F在边CB的延长线上，且AE=ED=BF，连接DF交AB于点G．若BC=4，则线段EG的长为__．

Answer 1

【答案】4.

【解析】

作DH∥CB交AB于H．只要证明AE=EH，BG=GH，即可推出EG=AB，由此即可解决问题．

作DH∥CB交AB于H．

∵∠C=90°，∠A=30°，∴∠ABC=60°．

∵DH∥BC，∴∠AHD=∠ABC=60°，∠DHG=∠FBG．

∵EA=ED，∴∠A=∠EDA=30°，∴∠HED=∠A+∠EDA=60°，∴△EDH是等边三角形，∴ED=EH=EA=DH=BF．

在△DHG和△FBG中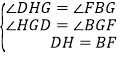，∵，∴△DHG≌△FBG，∴BG=HG．

∵HE=EA，∴EG=AB=BC=4．

故答案为：4．