题目内容
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?

【答案】(1)60.(2)y乙=90x﹣90;y甲=60x.()220km
【解析】
(1)根据图象确定出甲的路程与时间,即可求出速度;
(2)利用待定系数法即可解决问题;
(3)求出乙距A地240km时的时间,加上1,再乘以甲的速度即可得到结果.
(1)根据图象得:360÷6=60km/h.
故答案为:60.
(2)当1≤x≤5时,设y乙=kx+b,把(1,0)与(5,360)代入得: ,解得:k=90,b=﹣90,则y乙=90x﹣90;
,解得:k=90,b=﹣90,则y乙=90x﹣90;
当0<x≤6时,设y甲=mx,把(6,360)代入得到m=60,∴y甲=60x.
(3)∵乙与A地相距240km,且乙的速度为360÷(5﹣1)=90km/h,∴乙用的时间是240÷90= h,则甲与A地相距60×(
h,则甲与A地相距60×( +1)=220km.
+1)=220km.

练习册系列答案
相关题目
【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
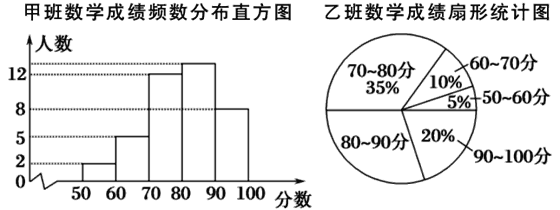
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________