题目内容
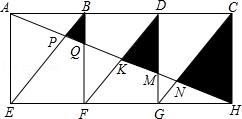
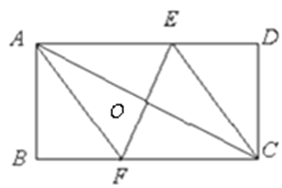
如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.连接BF、AC.

(1)求证:四边形ABFC是平行四边形;
(2)如果DE2=BE·CE,求证四边形ABFC是矩形.

(1)求证:四边形ABFC是平行四边形;
(2)如果DE2=BE·CE,求证四边形ABFC是矩形.
(1)证明见解析;(2)证明见解析.
试题分析:(1)连接BD,利用等腰梯形的性质得到AC=BD,再根据垂直平分线的性质得到DB=FB,从而得到AC=BF,然后证得AC∥BF,利用一组对边平行且相等判定平行四边形;
(2)利用题目提供的等积式和两直角相等可以证得两直角三角形相似,得到对应角相等,从而得到直角来证明有一个角是直角的平行四边形是矩形.
试题解析:(1)连接BD

∵梯形ABCD中,AD∥BC,AB=CD
∴AC=BD
∵DE⊥BC,EF=DE
∴BD=BF,CD=CF
∴AC=BF,AB=CF
∴四边形ABCF是平行四边形;
(2)∵DE2=BE•CE
∴
 ,
,∵∠DEB=∠DEC=90°,
∴△BDE∽△DEC,
∴∠CDE=∠DBE,
∴∠BFC=∠BDC=∠BDE+∠CDE=∠BDE+∠DBE=90°,
∴四边形ABFC是矩形.
考点: 1.等腰梯形的性质;2.全等三角形的判定与性质;3.平行四边形的判定与性质;4.相似三角形的判定与性质.

练习册系列答案
相关题目

 处,当△
处,当△ 为直角三角形时,BE的长为
为直角三角形时,BE的长为 
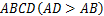 ,将纸片折叠一次,使点
,将纸片折叠一次,使点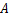 与
与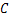 重合,再展开,折痕
重合,再展开,折痕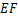 交
交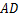 边于
边于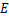 ,交
,交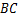 边于
边于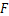 ,分别连接
,分别连接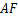 和
和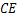 .
.
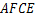 是菱形.
是菱形.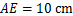 ,△
,△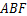 的面积为
的面积为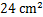 ,求△
,求△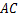 上是否存在一点
上是否存在一点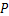 ,使得
,使得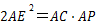 ?若存在,请说明点
?若存在,请说明点 中,
中, 6,
6, 8,
8, 平分∠
平分∠ 交
交 于点
于点 ,
,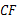 平分∠
平分∠ 交
交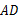 于点
于点 .
.
 为平行四边形;
为平行四边形;