��Ŀ����
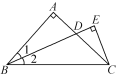
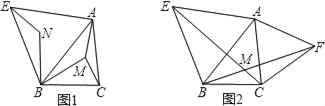
����Ŀ����ͼ������MΪ���������ABC������һ�㣬����AM��BM��CM����ABΪһ���������ȱ���������ABE����BM�Ƶ�B��ʱ����ת60���õ�BN������EN��
��1����֤����AMB�ա�ENB��
��2����AM+BM+CM��ֵ��С����Ƶ�MΪ��ABC�ķ����㣮����MΪ��ABC�ķ����㣬�����ʱ��AMB����BMC����CMA�Ķ�����
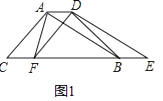
��3��С���������������õ�һ������������η�����ļ�㷽������ͼ�����ֱ�����ABC��AB��ACΪһ���������ȱ���ABE�͵ȱ���ACF������CE��BF���轻��ΪM�����M��Ϊ��ABC�ķ����㣮��˵���������������ݣ�
���𰸡���1������������2����BMC =120�㣻��AMB =120�㣻��AMC=120�㣻��3���߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ����㣮
��������
(1)��ϵȱ������ε����ʣ�����SAS��֤��AMB�ա�ENB��
(2)����MN����(1)�Ľ���֤����BMNΪ�ȱ������Σ�����BM=MN����AM+BM+CM=EN+MN+CM�����Ե�E��N��M��C�ĵ㹲��ʱ��AM+BM+CM��ֵ��С���Ӷ������ʱ��AMB����BMC����CMA�Ķ�����
(3)����(2)�з�����Ķ��壬����ABC�ķ��������߶�EC�ϣ�ͬ��Ҳ���߶�BF�ϣ�����߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ�����.
��1��֤�����ߡ�ABEΪ�ȱ������Σ�
��AB=BE����ABE=60�㣮
����MBN=60�㣬
���ABM=��EBN��
����AMB����ENB��
��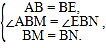
���AMB�ա�ENB��SAS����
��2������MN��
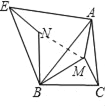
�ɣ�1��֪��AM=EN��
�ߡ�MBN=60�㣬BM=BN��
���BMNΪ�ȱ������Σ�
��BM=MN��
��AM+BM+CM=EN+MN+CM��
����E��N��M��C�ĵ㹲��ʱ��AM+BM+CM��ֵ��С��
��ʱ����BMC=180�㩁��NMB=120�㣻
��AMB=��ENB=180�㩁��BNM=120�㣻
��AMC=360�㩁��BMC����AMB=120�㣮
��3���ɣ�2��֪����ABC�ķ��������߶�EC�ϣ�ͬ��Ҳ���߶�BF�ϣ�
����߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ����㣮
�ʴ�Ϊ����1������������2����BMC =120������AMB =120������AMC=120������3���߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ����㣮

����Ŀ��ijʳƷ���������Ĵ�װʳƷ�г����Ʒ20�������ÿ���������Ƿ���ϱ�����������IJ��ֱַ���������������ʾ����¼���±���
��������IJ�ֵ |
|
| 0 | 1 | 3 | 6 |
�� �� | 1 | 4 | 3 | 4 | 5 | 3 |
��1��������Ʒ��ƽ�������ȱ���������٣�����ټ��ˣ�
��2����ÿ��������Ϊ450�ˣ�����������������Ƕ��٣�