题目内容
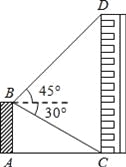
【题目】如图,已知AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )

A. 5° B. 15° C. 25° D. 35°
【答案】C
【解析】首先三角形的外角等于与它不相邻的两个内角的和可得∠A=∠EFB –∠E,再根据根据平行线的性质得到∠EFB=∠C.
解:∵AB∥CD,∠C=45°,
∴∠EFB=∠C=45°,
∵∠E=20°,
∴∠A=∠EFB –∠E =25°,
故选C.
“点睛”此题主要考查了平行线的性质,三角形的外角性质,关键是熟练掌握①平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等;②三角形的外角等于与它不相邻的两个内角的和,解题关键是求出∠EFB的度数,注意:两直线平行,同位角相等.

练习册系列答案
相关题目
【题目】某学习小组9名学生参加“数学竞赛”,他们的得分情况如表:
人数(人) | 1 | 3 | 4 | 1 |
分数(分) | 80 | 85 | 90 | 95 |
那么这9名学生所得分数的众数和中位数分别是( )
A. 90,90 B. 90,85 C. 90,87.5 D. 85,85