题目内容
【题目】两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:
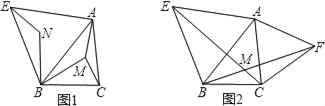
(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出S△ABC与S四边形AFBD的关系;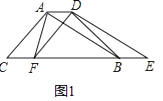
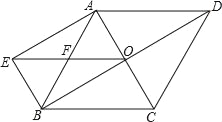
(2)如图2,当点F平移到线段BC的中点时,四边形AFBD是什么特殊四边形?请给出证明;
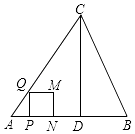
(3)当点F平移到线段BC的中点时,若四边形AFBD为正方形,猜想△ABC应满足什么条件?请直接写出结论:在此条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请在图3位置画出图形,并求出sin∠CGF的值.
【答案】
(1)解:S△ABC=S四边形AFBD,理由如下:
由题意可得:AD∥EC,
则S△ADF=S△ABD,
故S△ACF=S△ADF=S△ABD,
则S△ABC=S四边形AFBD;
(2)解:当点F平移到线段BC的中点时,四边形AFBD是平行四边形,理由如下:
∵F为BC的中点,
∴CF=BF,
∵CF=AD,
∴AD=BF,由平移可知AD∥BF,
∴四边形AFBD为平行四边形;
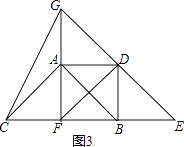
(3)解:如图3所示:△ABC为等腰直角三角形,即AB=AC,∠BAC=90°;理由如下:
由(2)得:四边形AFBD是平行四边形,
∵AB=AC,F为BC的中点,
∴AF⊥BC,
∴平行四边形AFBD为矩形,
∵∠BAC=90°,F为BC的中点,
∴AF= ![]() BC=BF,
BC=BF,
∴四边形AFBD是正方形;
设CF=k,则GF=EF=CB=2k,
由勾股定理得:CG= ![]() =
= ![]() k,
k,
sin∠CGF= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)利用平行线的性质以及三角形面积关系得出答案;(2)证出AD=BF,由平移可知AD∥BF,利用平行四边形的判定得出四边形AFBD为平行四边形即可;(3)根据题意画出图形,由等腰三角形的性质得出AF⊥BC,证出平行四边形AFBD为矩形,由直角三角形斜边上的中线性质得出AF= ![]() BC=BF,得出四边形AFBD是正方形;设CF=k,则GF=EF=CB=2k,由勾股定理求出CG,利用sin∠CGF=
BC=BF,得出四边形AFBD是正方形;设CF=k,则GF=EF=CB=2k,由勾股定理求出CG,利用sin∠CGF= ![]() 求出即可.
求出即可.