Question

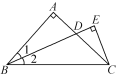
【题目】如图，在△ABC中，AB＝AC，∠BAC＝90°，∠1＝∠2，CE⊥BD交BD的延长线于点E.求证：BD＝2CE.

Answer 1

【答案】证明见解析.

【解析】

延长CE、BA交于F，根据角边角定理，证明△BEF≌△BEC，进而得到CF=2CE的关系．再证明∠ACF=∠1，根据角边角定理证明△ACF≌△ABD，得到BD=CF，至此问题得解．

证明：分别延长BA，CE交于点F.

∵BE⊥CE，

∴∠BEF＝∠BEC＝90°.

又∵∠1＝∠2，BE＝BE，

∴△BEF≌△BEC(ASA)，

∴CE＝FE＝CF.

∵∠1＋∠F＝90°，∠ACF＋∠F＝90°，

∴∠1＝∠ACF.又∵AB＝AC，∠BAD＝∠CAF＝90°，

∴△ABD≌△ACF(ASA)，

∴BD＝CF，

∴BD＝2CE