8、解:(Ⅰ)设甲、乙两人考试合格的事件分别为A、B,则
P(A)= =
= ,P(B)=
,P(B)= . ………3分
. ………3分
因为事件A、B相互独立,
∴甲、乙两人考试均合格的概率为  ……………………5分
……………………5分
答:甲、乙两人考试均合格的概率为 . …………………………6分
. …………………………6分
(Ⅱ)依题意,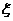 =0,1,2,3,………………7分
=0,1,2,3,………………7分
 ,
,  ,
,
 ,
,  ……………………………9分
……………………………9分
甲答对试题数ξ的概率分布如下:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
 |
 |
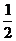 |
 |
甲答对试题数ξ的数学期望

 .
……………………12分
.
……………………12分
7、解(I) ……………………………………………………2分
……………………………………………………2分
 ,
, ,
, ……8分
……8分
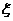 |
2 |
6 |
10 |
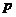 |
 |
 |
 |
所以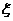 的概率分布列为:
的概率分布列为:
………………………10分
(II)由(I)知, ………………………12分
………………………12分
所以抽奖人获利的数学期望为: 元。 ………………………14分
元。 ………………………14分
6、解:(1)从50名教师随机选出2名的方法数为
选出2人使用版本相同的方法数为
故2人使用版本相同的概率为:
 …………………………5分
…………………………5分
(2)∵ ,
, 

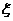 |
0 |
1 |
2 |
|
P |
 |
 |
 |
∴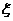 的分布列为
的分布列为
………………10分
∴ ……………………12分
……………………12分
 (2009珠海)已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( C )
(2009珠海)已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( C ) B.
B.
 D.
D.
 是两个不同的平面,m,n是两条不同的直线,给出下列命题:
是两个不同的平面,m,n是两条不同的直线,给出下列命题: ;
; ;
;  相交;
相交;
 (2009北江中学)如图是一个空间几何体的主视图、左视图、俯视图,如果主视图、左视图所对应的三角形皆为边长为2的正三角形,主视图对应的四边形为正方形,那么这个几何体的体积为( )B
(2009北江中学)如图是一个空间几何体的主视图、左视图、俯视图,如果主视图、左视图所对应的三角形皆为边长为2的正三角形,主视图对应的四边形为正方形,那么这个几何体的体积为( )B B.
B. C.
C. D.不确定
D.不确定 则
则 B.m∥n,m⊥α,则n⊥α
B.m∥n,m⊥α,则n⊥α (2009番禺)一个几何体的三视图如右图,其中主视图和左视图都是边长为1的正三角形,那么这个几何体的侧面积为( )A
(2009番禺)一个几何体的三视图如右图,其中主视图和左视图都是边长为1的正三角形,那么这个几何体的侧面积为( )A B.
B.  C.
C. D.
D.
 、
、 与平面
与平面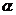 、
、 的命题中,真命题是( )B
的命题中,真命题是( )B ,且
,且 ,则
,则 (B)若
(B)若 ,且
,且 ,则
,则 ,且
,且 ,则
,则 (D)若
(D)若 (2009揭阳)某师傅需用合板制作一个工作台,工作台由主体和附属两部分组成,主体部分全封闭,附属部分是为了防止工件滑出台面而设置的三面护墙,其大致形状的三视图如右图所示(单位长度:
cm), 则按图中尺寸,做成的工作台用去的合板的面积为(制作过程合板的损耗和合板厚度忽略不计)( )D
(2009揭阳)某师傅需用合板制作一个工作台,工作台由主体和附属两部分组成,主体部分全封闭,附属部分是为了防止工件滑出台面而设置的三面护墙,其大致形状的三视图如右图所示(单位长度:
cm), 则按图中尺寸,做成的工作台用去的合板的面积为(制作过程合板的损耗和合板厚度忽略不计)( )D B.
B. 
 D.
D. 