5、解:(Ⅰ)设甲获第一、丙获第二、乙获第三为事件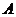 ,
,
则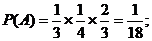 ············································································ 6分
············································································ 6分
(Ⅱ)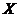 可能的取值为
可能的取值为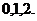
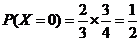 ,
,
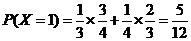 ,
,
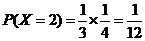 ,··········································································· 12分
,··········································································· 12分
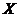 |
0 |
1 |
2 |
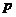 |
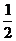 |
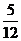 |
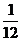 |
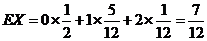 ······························································· 14分
······························································· 14分
4、解:(1)设掷两颗正方体骰子所得的点数记为(x,y),其中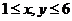 ,
,
则获一等奖只有(6,6)一种可能,其概率为: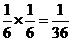 ; …………2分
; …………2分
获二等奖共有(6,5)、(5,6)、(4,6)、(6,4)、(5,5)共5种可能,其概率为: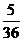 ;
;
…………5分
设事件A表示“同行的三位会员一人获一等奖、两人获二等奖”,则有:
P(A)=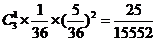 ;
…………6分
;
…………6分
|
ξ |
30-a |
-70 |
0 |
30 |
|
p |
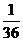 |
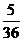 |
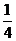 |
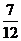 |
(2)设俱乐部在游戏环节收益为ξ元,则ξ的可能取值为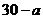 ,
,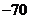 ,0,
,0,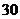 ,…7分
,…7分
其分布列为:
则:Eξ=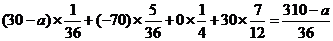 ; …………11分
; …………11分
由Eξ=0得:a=310,即一等奖可设价值为310 元的奖品。 …………12分
3、解: 用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,
且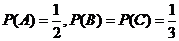 .------------------------------------------------------2分
.------------------------------------------------------2分
(1)至少有1人面试合格的概率是
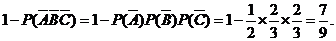 ----------------------4分
----------------------4分
(2)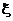 的可能取值为0,1,2,3.----------------------------------------------------------5分
的可能取值为0,1,2,3.----------------------------------------------------------5分
∵ 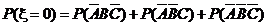
=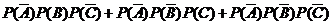
=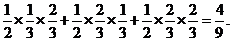 ---------------------------6分
---------------------------6分
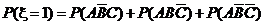
=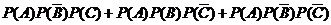
=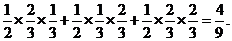 --------------------------------7分
--------------------------------7分
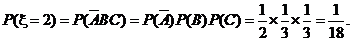 ---------------------8分
---------------------8分
 ----------------------9分
----------------------9分
∴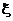 的分布列是
的分布列是
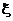 |
0 |
1 |
2 |
3 |
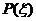 |
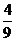 |
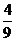 |
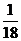 |
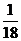 |
--------10分
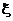 的期望
的期望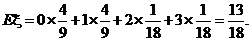 ----------------------------------------12分
----------------------------------------12分
2、解: 由题意可知,飞镖落在靶内各个区域的概率与它们的面积成正比,而与它们的质量和形状无关。
由圆的半径值可得到三个同心圆的半径之比为3:2:1,面积比为9:4:1
所以8环区域、9环区域、10环区域的面积比为5:3:1 ………3分
则掷得8环、9环、10环的概率分别设为5k,3k,k
根据离散型随机变量分布列的性质有0.1+5k+3k+k=1
解得k=0.1 ………6分
得到离散型随机变量x的分布列为
|
x |
0 |
8 |
9 |
10 |
|
P |
0.1 |
0.5 |
0.3 |
0.1 |
………9分
Ex=0×0.1+8×0.5+9×0.3+10×0.1=7.7 ………12分
6、(2009朝阳一中)某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为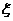 ,求随机变量
,求随机变量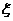 的变分布列和数学期望。
的变分布列和数学期望。
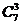 种选法,.选出的3种商品中没有日用商品的选法有
种选法,.选出的3种商品中没有日用商品的选法有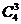 种, ……1分.
种, ……1分.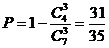 .……4分
.……4分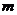 ,2
,2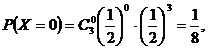 ……7分
……7分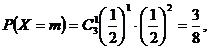 ……8分
……8分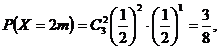 ……9分
……9分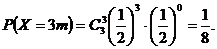 ……10分
……10分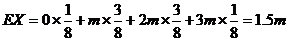 .……12分
.……12分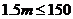 ,所以
,所以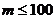 ,……13分.
,……13分.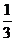 ,甲胜丙的概率为
,甲胜丙的概率为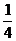 ,乙胜丙的概率为
,乙胜丙的概率为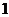 分,负者得
分,负者得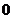 分,设在此次比赛中甲得分数为
分,设在此次比赛中甲得分数为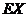 .
.