2.在恒温恒容条件下,对于反应前后气体分子数不变的可逆反应,只要反应物(或生成物)的物质的量的比例与原平衡相同,两平衡等效。
 H2(g)+I2(g) 2HI(g)
H2(g)+I2(g) 2HI(g)
途径1 2 mol 1mol 0
途径2 1mol 0 1mol
途径3 4mol 2mol 0
途径4 3mol 1mol 2mol
[例题2]在一固定体积的密闭容器中,保持一定温度进行以下反应H2(g)+ I2(g)  2HI(g)已知加入1mol H2(g)和21mol I2(g)时,达到平衡后生成amol HI(g)。在相同体条件下,保持平衡时各组分的体积分数不变,根据下表编号①-③的状态填空
2HI(g)已知加入1mol H2(g)和21mol I2(g)时,达到平衡后生成amol HI(g)。在相同体条件下,保持平衡时各组分的体积分数不变,根据下表编号①-③的状态填空
|
已知 编号 |
起始状态物质的量n/mol |
平衡时HI(g)的物质的量n/mol |
||
|
H2(g) |
I2(g) |
HI(g) |
||
|
1 |
2 |
0 |
a |
|
|
① |
2 |
4 |
0 |
|
|
② |
|
|
1 |
0.5a |
|
③ |
m |
g(g ≥2m) |
|
|
 2NH3
2NH3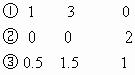 ;则①②③的量相当。
;则①②③的量相当。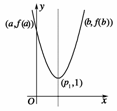
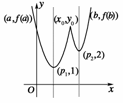
 显然p1<x0=P2-[(p2-p1)-log32]<p2,这表明x0在p1与p2之间.
显然p1<x0=P2-[(p2-p1)-log32]<p2,这表明x0在p1与p2之间.