10.(2000春全国)已知抛物线y2=4px(p>0),O为顶点,A、B为抛物线上的两动点,且满足OA⊥OB,如果OM⊥AB于M点,求点M的轨迹方程.
分析:点M随着A、B两点的变化而变化,点M是OM与AB的交点,而A、B为抛物线上的动点,点M与A、B的直接关系不明显,因此需引入参数.
解法一:设M(x0,y0),则kOM= ,kAB=-
,kAB=- ,
,
直线AB方程是y=- (x-x0)+y0.
(x-x0)+y0.
由y2=4px可得x= ,代入上式整理得
,代入上式整理得
x0y2-(4py0)y-4py02-4px02=0. ①
此方程的两根y1、y2分别是A、B两点的纵坐标,
∴A( ,y1)、B(
,y1)、B( ,y2).
,y2).
∵OA⊥OB,∴kOA·kOB=-1.
∴ ·
· =-1.∴y1y2=-16p2.
=-1.∴y1y2=-16p2.
根据根与系数的关系,由①可得
y1·y2= ,
,
∴ =16p2.
=16p2.
化简,得x02+y02-4px0=0,
即x2+y2-4px=0(除去原点)为所求.
∴点M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.
解法二:设M(x,y),直线AB方程为y=kx+b,
由OM⊥AB得k=- .
.
由y2=4px及y=kx+b消去y,得
k2x2+x(2kb-4p)+b2=0.
所以x1x2= .消去x,得ky2-4py+4pb=0.
.消去x,得ky2-4py+4pb=0.
所以y1y2= .由OA⊥OB,
.由OA⊥OB,
得y1y2=-x1x2,
所以 =-
=- ,b=-4kp.
,b=-4kp.
故y=kx+b=k(x-4p).
用k=- 代入,得
代入,得
x2+y2-4px=0(x≠0).
解法三:设点M的坐标为(x,y),直线OA的方程为y=kx,
|
 x.
x.

|
y2=4px,
 类似地可得B点的坐标为(4pk2,-4pk),
类似地可得B点的坐标为(4pk2,-4pk),
从而知当k≠±1时,
kAB= =
= .
.
故得直线AB的方程为y+4pk= (x-4pk2),
(x-4pk2),
即( -k)y+4p=x,
①
-k)y+4p=x,
①
直线OM的方程为y=-( -k)x. ②
-k)x. ②
可知M点的坐标同时满足①②,
由①及②消去k便得4px=x2+y2,
即(x-2p)2+y2=4p2,但x≠0,
当k=±1时,容易验证M点的坐标仍适合上述方程.
故点M的轨迹方程为(x-2p)2+y2=4p2(x≠0),
它表示以点(2p,0)为圆心,以2p为半径的圆.
[探索题](2006辽宁)
已知点 ,
,
 是抛物线
是抛物线 上的两个动点,
上的两个动点, 是坐标原点,向量
是坐标原点,向量 ,
, 满足
满足 .设圆
.设圆 的方程为
的方程为
(I)证明线段 是圆
是圆 的直径;
的直径;
(II)当圆C的圆心到直线x-2y=0的距离的最小值为 时,求P的值。
时,求P的值。
(I)证法一:∵ ,
,
∴ ,
,
即 ,
,
整理得 .
.
∴ 1
1
设点 是以线段
是以线段 为直径得圆上得任意一点,则
为直径得圆上得任意一点,则
即
展开上式并将1带入得
故线段 是圆
是圆 的直径.
的直径.
证法二:同法一得: 1
1
以 AB 为直径的圆的方程是
 ,
,
展开,并将①代入得
所以线段 AB 是圆 C 的直径
(II)解法一:设圆 的圆心为
的圆心为 则
则
∵
∴
又∵ =0
=0
∴ ∴
∴
∵ ,∴
,∴ , ∴
, ∴
∴
 ,
,
所以圆心的轨迹方程为:
设圆心 到直线
到直线 的距离为
的距离为 ,则
,则

当 时,
时, 有最小值
有最小值 ,由题设得
,由题设得 ,∴
,∴
解法二:同法一得:圆心的轨迹方程为:
设直线 与
与 的距离为
的距离为 ,则
,则

当 与
与 仅有一个公共点时,
仅有一个公共点时,
 该点到
该点到 的距离最小,最小值为
的距离最小,最小值为 ,
,
由 ②
③
消x得 ,
,
由
得 (∵
(∵ )
)
解法三:设圆 的圆心为
的圆心为 ,则
,则
若圆心 到直线
到直线 的距离为
的距离为 ,那
,那
∵
∴
又∵ ,
,  ,
,
∵ ,∴
,∴
∴


当 时,
时, 有最小值
有最小值 ,由题设得
,由题设得 ,
,
∴
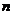 项和公式.解答题作为压轴题的可能性较大,与不等式、数学归纳法、函数等一起综合考查学生运用数学知识进行归纳、总结、推理、论证、运算等能力以及分析问题、解决问题的能力.具体地:
项和公式.解答题作为压轴题的可能性较大,与不等式、数学归纳法、函数等一起综合考查学生运用数学知识进行归纳、总结、推理、论证、运算等能力以及分析问题、解决问题的能力.具体地: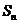 与
与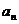 的关系一直是高考的热点,求数列的通项公式是最为常见的题目,要切实注意
的关系一直是高考的热点,求数列的通项公式是最为常见的题目,要切实注意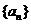 是等差数列,
是等差数列, ,
, ,则该数列前10项和
,则该数列前10项和 等于( )
等于( ) ,则由已知得
,则由已知得 ,
, .
. 的前n项和为
的前n项和为 ,则
,则 ( )
( ) ,公差
,公差 ,
, .[答案]A.
.[答案]A. 沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从
沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从 这点开始跳,则经2009次跳后它停在的点所对应的数为( )
这点开始跳,则经2009次跳后它停在的点所对应的数为( ) B.
B. C.
C. D.
D.
 中
中 ,则其前3项的和
,则其前3项的和 的取值范围是( )
的取值范围是( )  B.
B. C.
C. D.
D.
 ,
, ,由
,由 或
或 ,所以取值范围为
,所以取值范围为 ,则
,则

 .
. 满足
满足 ,则
,则 ,
,
 ,则
,则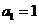 ,
,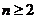 时,
时, .
. .
. 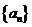 中,
中, ,
, (
( 是不为零的常数,
是不为零的常数, ),且
),且 成等比数列.
成等比数列. 的前
的前 .
. ,
, ,
, ,
, ,
,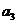 成等比数列,
成等比数列, ,
,
 或
或 .
.
 时,由于
时,由于 ,
, ,
,
 ,
, .
.
 .
.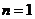 时,上式也成立,
时,上式也成立, .
.


 ……①
……① ……②
……②
 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3…. 求证数列
求证数列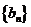 是等比数列;
是等比数列; 

 的前n项和,是否存在实数
的前n项和,是否存在实数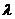 ,使得数列
,使得数列 为等差数列?若存在,试求出
为等差数列?若存在,试求出




 是以
是以 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列.








 ,使数列
,使数列 是等差数列.
是等差数列.



 、
、 是常数
是常数



 当且仅当
当且仅当 ,即
,即





 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数
(1)用
为正实数
(1)用 表示
表示 ;
(2)
;
(2) ,若
,若 ,试证明数列
,试证明数列 ,记数列
,记数列 的前
的前 ,求
,求 ,所以在曲线上点
,所以在曲线上点 处的切线方程为
处的切线方程为 ,即
,即
 ,得
,得 ,即
,即
 ,所以
,所以


 ,所以数列
,所以数列 ---8分
---8分 

 ,故数列
,故数列 的通项公式为
的通项公式为
 ①
① ①
① 的
的 ②
② ②得
②得
 .
.  (m为常数,m>0且
(m为常数,m>0且 ),设
),设 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.  ,且数列{bn}的前n项和Sn,当
,且数列{bn}的前n项和Sn,当 时,求Sn;
时,求Sn; ,问是否存在m,使得{cn}中每一项恒小于它后面的项?
,问是否存在m,使得{cn}中每一项恒小于它后面的项? 即
即

 ∵m>0且
∵m>0且 ∴数列{an}是以m4为首项,m2为公比的等比数列
∴数列{an}是以m4为首项,m2为公比的等比数列
 ,
,
 ①
①
 ②
② 



 …10分
…10分
 对一切
对一切 成立,即
成立,即  对一切
对一切
 成立;
成立;

 对一切
对一切  ,
, , 考虑到0<m<1, ∴0<m<
, 考虑到0<m<1, ∴0<m<
 或m>1时,数列{cn}中每一项恒小于它后面的项.
或m>1时,数列{cn}中每一项恒小于它后面的项.  ,
, ,则
,则 ( )
( ) ,
, ,故
,故 .
. 是等比数列,
是等比数列, ,则
,则 =( )
=( ) )
(B)16(
)
(B)16( )
)
 (
( ,解得
,解得 ,
, 仍是等比数列:其首项是
仍是等比数列:其首项是 公比为
公比为 ,
, .
. .若
.若 是
是 的等比中项,则
的等比中项,则 ( )
( ) ,
,
 ,则
,则 ,
, (舍负).
(舍负). 个,因此第n 行第3 个数是全体正整数中第
个,因此第n 行第3 个数是全体正整数中第 .
. 、
、 的两个根,且
的两个根,且 及
及 (n≥4)(不必证明);
(n≥4)(不必证明); .
. ,所以
,所以 ,所以
,所以 ;当k=3时,
;当k=3时, ,所以
,所以 ;
; ,所以
,所以 ;
; ,所以
,所以

 .
. ,
, .
. ,求数列
,求数列

 ,
, .
. 时也满足上式,
时也满足上式, .
. (II)
(II)  ,
,
 ,
, ,
,
 ,所以
,所以 .
. 为实数
为实数 对任意
对任意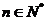 成立的充分必要条件是
成立的充分必要条件是 ;
; ,证明:
,证明: ;
;
 ,
, ,即
,即 .假设
.假设
 ,且
,且
 ,由数学归纳法知
,由数学归纳法知 ,结论成立
,结论成立
 ,由(1)知
,由(1)知 ,所以
,所以  且
且 



 ,结论成立
,结论成立


 .
. ,
, ),
), 如图,O为坐标原点,直线
如图,O为坐标原点,直线 在
在 轴和
轴和 轴上的截距分别是
轴上的截距分别是 和
和 ,且交抛物线
,且交抛物线 于
于 、
、 两点.
两点. ;
; 时,求
时,求 的大小.
的大小. ①
① ②
②

 在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图4所示).
在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图4所示). …(1)
…(1) ,代入(2)化简得
,代入(2)化简得
 ,
, .
.


 即
即 时,
时, .
.
 ①
① ②
②

