2、简谐运动
(1)弹簧振子:一个轻质弹簧联接一个质点,弹簧的另一端固定,就构成了一个弹簧振子。
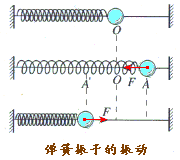
(2)振动形成的原因
①回复力:振动物体受到的总能使振动物体回到平衡位置,且始终指向平衡位置的力,叫回复力。
振动物体的平衡位置也可说成是振动物体振动时受到的回复力为零的位置。
②形成原因:振子离开平衡位置后,回复力的作用使振了回到平衡位置,振子的惯性使振子离开平衡位置;系统的阻力足够小。
(3)振动过程分析
|
振子的运动 |
A→O |
O→A′ |
A′→O |
O→A |
|
对O点位移的方向怎样?大小如何变化? |
向右 减小 |
向左 增大 |
向左 减小 |
向右 增大 |
|
回复力的方向怎样?大小如何变化? |
向左 减小 |
向右 增大 |
向右 减小 |
向左 增大 |
|
加速度的方向怎样?大小如何变化? |
向左 减小 |
向右 增大 |
向右 减小 |
向左 增大 |
|
速度的方向怎样?大小如何变化? |
向左 增大 |
向左 减小 |
向右 增大 |
向右 减小 |
|
动量的方向怎样?大小如何变化? |
向左 增大 |
向左 减小 |
向右 增大 |
向右 减小 |
|
振子的动能 |
增大 |
减小 |
增大 |
减小 |
|
弹簧的势能 |
减小 |
增大 |
减小 |
增大 |
|
系统总能量 |
不变 |
不变 |
不变 |
不变 |
(4)简谐运动的力学特征
①简谐运动:物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫做简谐运动。
②动力学特征:回复力F与位移x之间的关系为
F=-kx
式中F为回复力,x为偏离平衡位置的位移,k是常数。简谐运动的动力学特征是判断物体是否为简谐运动的依据。
③简谐运动的运动学特征
a=- x
加速度的大小与振动物体相对平衡位置的位移成正比,方向始终与位移方向相反,总指向平衡位置。
简谐运动加速度的大小和方向都在变化,是一种变加速运动。简谐运动的运动学特征也可用来判断物体是否为简谐运动。
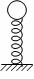
例题:试证明在竖直方向的弹簧振子做的也是简谐振运动。
证明:设O为振子的平衡位置,向下方向为正方向,此时弹簧形变量为x0,根据胡克定律得
x0=mg/k
当振子向下偏离平衡位置x时,回复力为
F=mg-k(x+x0)
则F=-kx
所以此振动为简谐运动。
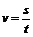 ,速度不随时间变化。
,速度不随时间变化。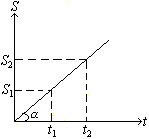
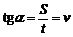 )所以由位移图象不仅可以求出速度, 还可直接读出任意时间内的位移(t1时间内的位移S1)以及可直接读出发生任一位移S2所需的时间t2。
)所以由位移图象不仅可以求出速度, 还可直接读出任意时间内的位移(t1时间内的位移S1)以及可直接读出发生任一位移S2所需的时间t2。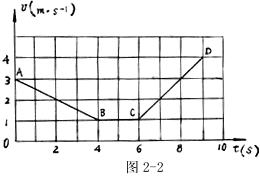

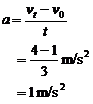
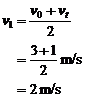
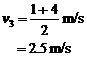
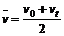 ,只对匀变速直线运动才适用。
,只对匀变速直线运动才适用。 ②当Δt 0时,平均速度的极限为瞬时速度。
②当Δt 0时,平均速度的极限为瞬时速度。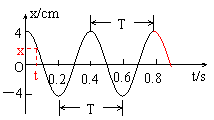 ①判断振动的性质
①判断振动的性质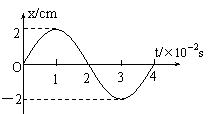 ①该振动的振幅是_______,周期是________。
①该振动的振幅是_______,周期是________。 ①全振动
①全振动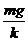
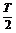 的整数倍
的整数倍 T,故A、B均不对.对C选项,因为△t=T,所以t和t +△t时刻振子的位移
、速度、加速度等都将周期性重复变化,加速度相同,C对.对D选 ,△t=
T,故A、B均不对.对C选项,因为△t=T,所以t和t +△t时刻振子的位移
、速度、加速度等都将周期性重复变化,加速度相同,C对.对D选 ,△t=