例1 已知角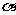 的终边经过点P(2,-3)(如图),求
的终边经过点P(2,-3)(如图),求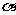 的六个三角函数值.
的六个三角函数值.
解:∵x=2,y=-3
∴
于是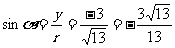
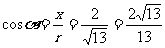
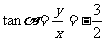
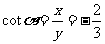
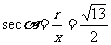
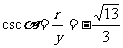
例2求下列各角的六个三角函数值.
(1)0
(2)π (3)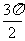 (4)
(4) 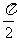
解:(1)因为当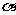 =0时,x=r,y=0,所以
=0时,x=r,y=0,所以
sin0=0 cos0=1 tan0=0 cot0不存在
sec0=1 csc0不存在
(2)因为当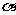 =π时,x=-r,y=0,所以
=π时,x=-r,y=0,所以
sinπ=0 cosπ=-1 tanπ=0 cotπ不存在
secπ=-1 cscπ不存在
(3)因为当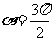 时,x=0,y=-r,所以
时,x=0,y=-r,所以

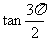 不存在
不存在 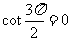
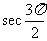 不存在
不存在 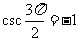
(4)当a=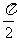 时
时 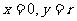 ,所以
,所以
sin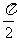 =1 cos
=1 cos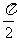 =0 tan
=0 tan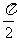 不存在 cot
不存在 cot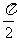 =0
=0
sec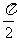 不存在 csc
不存在 csc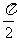 =1
=1
例3填表:
|
a |
0° |
30° |
45° |
60° |
90° |
120° |
135° |
150° |
180° |
270° |
360° |
|
弧度 |
|
|
|
|
|
|
|
|
|
|
|
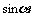 |
|
|
|
|
|
|
|
|
|
|
|
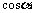 |
|
|
|
|
|
|
|
|
|
|
|
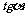 |
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
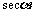 |
|
|
|
|
|
|
|
|
|
|
|
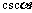 |
|
|
|
|
|
|
|
|
|
|
|
例4 ⑴ 已知角a的终边经过P(4,-3),求2sina+cosa的值
⑵已知角a的终边经过P(4a,-3a),(a¹0)求2sina+cosa的值
解:⑴由定义 :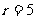 sina=-
sina=-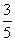 cosa=
cosa=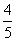 ∴2sina+cosa=-
∴2sina+cosa=-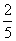
⑵若
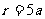 则sina=-
则sina=-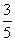 cosa=
cosa=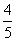 ∴2sina+cosa=-
∴2sina+cosa=-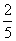
若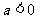
 则sina=
则sina=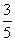 cosa=-
cosa=-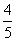 ∴2sina+cosa=
∴2sina+cosa=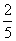
例5 求函数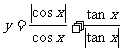 的值域
的值域
解: 定义域:cosx¹0 ∴x的终边不在x轴上
又∵tanx¹0 ∴x的终边不在y轴上
当x是第Ⅰ象限角时,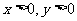 cosx=|cosx|
tanx=|tanx| ∴y=2
cosx=|cosx|
tanx=|tanx| ∴y=2
当x是第Ⅱ象限角时,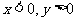 |cosx|=-cosx |tanx|=-tanx ∴y=-2
|cosx|=-cosx |tanx|=-tanx ∴y=-2
当x是第Ⅲ象限角时, 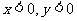 |cosx|=-cosx |tanx|=tanx ∴y=0
|cosx|=-cosx |tanx|=tanx ∴y=0
当x是第Ⅳ象限角时, 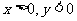 |cosx|=cosx |tanx|=-tanx ∴y=0
|cosx|=cosx |tanx|=-tanx ∴y=0
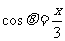 ,求sinθ和tanθ的值.
,求sinθ和tanθ的值.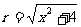 ,又
,又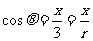 ,即rx=3x
,即rx=3x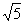 .
.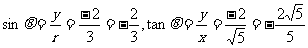
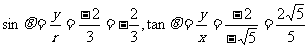 .
.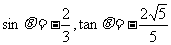
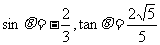
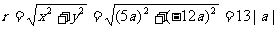
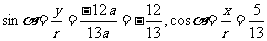 ,
,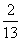 ;
; 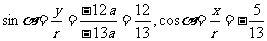 .
.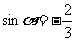 ,则y的值是 .答案:
,则y的值是 .答案: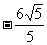

 而x,y的正负是随象限的变化而不同,故三角函数的符号应由象限确定.
而x,y的正负是随象限的变化而不同,故三角函数的符号应由象限确定.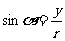 ,因为r>0,所以
,因为r>0,所以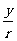 恒有意义,即
恒有意义,即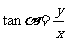 ,因为x=0时,
,因为x=0时,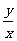 无意义,即tan
无意义,即tan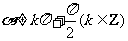 .从而有
.从而有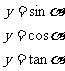
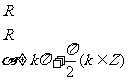
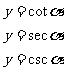
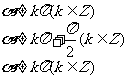
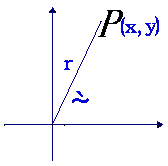 比值
比值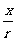 叫做
叫做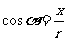
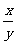 叫做
叫做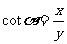
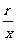 叫做
叫做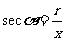
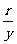 叫做
叫做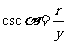
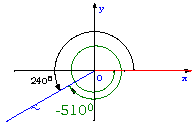 根据相似三角形的知识,对于终边不在坐标轴上确定的角
根据相似三角形的知识,对于终边不在坐标轴上确定的角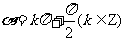 时,终边上任意一点P的横坐标x都为0,所以tan
时,终边上任意一点P的横坐标x都为0,所以tan