8.设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
t |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωx+φ)的图象,下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
A.y=12+3sint,t∈[0,24]
B.y=12+3sin(t+π),t∈[0,24]
C.y=12+3sint,t∈[0,24]
D.y=12+3sin(t+),t∈[0,24]
解析:代入坐标验证即可选A.
答案:A
|
题组四 |
函数y=Asin(ωx+φ)的综合应用 |
6.(2010·黄冈模拟)已知函数f(x)=Acos(ωx+φ)的图角如图所示,f()=-,则f(0)=________.
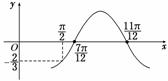
解析:由图象可得最小正周期为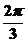 .
.
所以f(0)=f(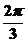 ),注意到
),注意到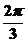 与
与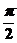 关于
关于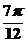 对称,
对称,
故f(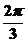 )=-f(
)=-f(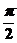 )=
)=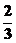 .
.
答案: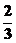
|
题组三 |
三角函数模型的应用 |
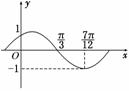
3.已知函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,则ω=________.
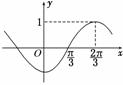
解析:由题意设函数周期为T,则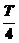 =
=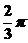 -
-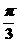 =
=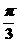 ,
,
∴T=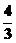 π,
π,
∴ω=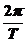 =
=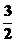 .
.
答案: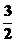
|
题组二 |
求三角函数y=Asin(ωx+φ)的解析式 |
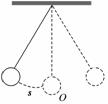 如图,单摆从某点开始来回摆动,离开平衡位置O的距离
如图,单摆从某点开始来回摆动,离开平衡位置O的距离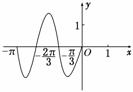
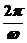 =
= 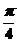 ×4,ω=2,当x=
×4,ω=2,当x=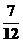 π时,2(
π时,2(