19. (本小题满分13分) 已知函数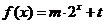 的图象经过点A(1,1),B(2,3) ,及C(n,Sn),Sn为数列
的图象经过点A(1,1),B(2,3) ,及C(n,Sn),Sn为数列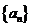 的前n项的和,
的前n项的和, (1) 求Sn及an (2)
设bn=log2an-1,数列
(1) 求Sn及an (2)
设bn=log2an-1,数列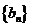 的前n项和为Tn ,求证:
的前n项和为Tn ,求证: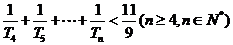
解 (1)由 2m+t=1得 t= -1
4m+t=3 m=1 2分
所以 f(x)=2x -1 则 Sn=2n -1  4分
4分
当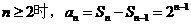
当n=1时,a1=S1=1满足上式,所以an=2n-1 ( )
6 分
)
6 分
(2)证明:因为bn=log2an-1=n-2
所以 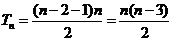 8分
8分
所以 ,当n≥4时,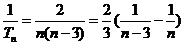 10分
10分
所以 13分
13分
20(本小题满分13分)
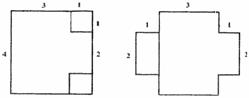
在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的长方体无盖容器(只有一个下底面和侧面的长方体).该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求的方案,简单说明操作过程和理由.
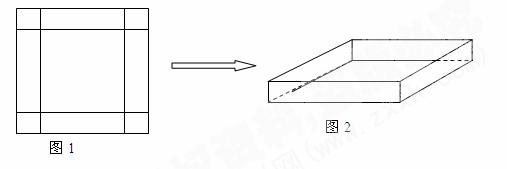
解:(1)设切去正方形边长为x,则焊接成的长方体的底面边长为4-2x,高为x ,
所以V1= (4-2x)2·x = 4(x3-4x2 + 4x) (0<x<2) .……….. ……….. ……….. 4分
∴V1/ = 4(3x2-8x + 4),……….. ……….. ……….. ……….. ……….. ………. ….5分
令V1/ = 0,即4(3x2-8x + 4) = 0,解得x1 = ,x2 = 2 (舍去) .……….. ………7分
∵ V1在(0,2)内只有一个极值,
∴ 当x = 时,V1取得最大值.<5,即不符合要求. ….…. …. 9分
(2)重新设计方案如下:
如图①,在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;如图③,将图②焊成长方体容器.新焊长方体容器底面是一个长方形,长为3,宽为2,此长方体容积V2 = 3×2×1 = 6,显然V2>5.
故第二种方案符合要求.
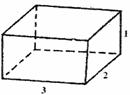
图① 图② 图③
…. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. ….13分
注:第二问答案不唯一。
21(本小题满分13分)
已知函数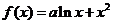 (为实常数).
(为实常数).
(Ⅰ) 若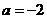 ,求证:函数
,求证:函数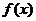 在
在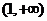 上是增函数;
上是增函数;
(Ⅱ) 若存在x∈[1,e],使得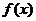 ≤
≤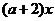 成立,求实数的取值范围.
成立,求实数的取值范围.
(Ⅲ) 求函数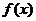 在[1,e]上的最小值及相应的x值;
在[1,e]上的最小值及相应的x值;
解:(Ⅰ)当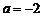 时,
时, ,当
,当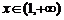 ,
, ,
,
故函数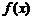 在
在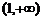 上是增函数.………………………………………………………………………2分
上是增函数.………………………………………………………………………2分
(Ⅱ) 不等式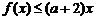 , 可化为
, 可化为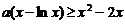 .∵
.∵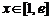 ,
,
∴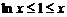 且等号不能同时取,所以
且等号不能同时取,所以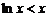 ,即
,即 ,因而
,因而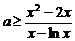 (
(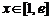 )… 4 分
)… 4 分
令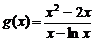 (
(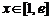 ),又
),又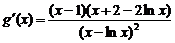 ……………………………………
……………………………………
当 时,
时,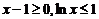 ,
,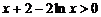 ,…………………………………………………6分
,…………………………………………………6分
从而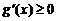 (仅当x=1时取等号),所以
(仅当x=1时取等号),所以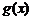 在
在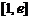 上为增函数 ………………………………
上为增函数 ………………………………
故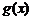 的最小值为
的最小值为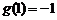 ,所以实数的取值范围是
,所以实数的取值范围是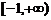 ……………………………………8分
……………………………………8分
(Ⅲ) 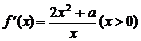 ,当
,当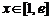 ,
, .………………………………
.………………………………
若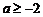 ,
,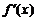 在
在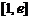 上非负(仅当
上非负(仅当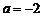 ,
,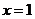 时,
时,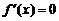 ),故函数
),故函数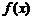 在
在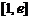 上是增函数,此时
上是增函数,此时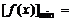
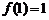 . …………………………………………9分
. …………………………………………9分
若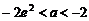 ,当
,当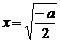 时,
时,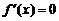 ;当
;当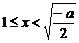 时,
时,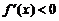 ,此时
,此时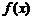 是减函数; 当
是减函数; 当 时,
时,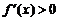 ,此时
,此时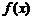 是增函数.故
是增函数.故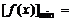
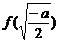
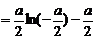 … 11…分
… 11…分
若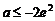 ,
,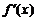 在
在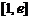 上非正(仅当
上非正(仅当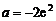 ,
,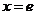 时,
时,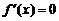 ),故函数
),故函数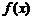 在
在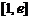 上是减函数,此时
上是减函数,此时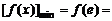
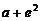 . …………………………………………………………12分…
. …………………………………………………………12分…
综上可知,当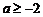 时,
时,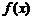 的最小值为1,相应的x值为1;
的最小值为1,相应的x值为1;
当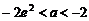 时,
时,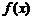 的最小值为
的最小值为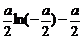 ,相应的x值为
,相应的x值为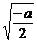 ;
;
当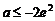 时,
时,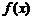 的最小值为
的最小值为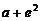 ,相应的值为……………………………………………13分
,相应的值为……………………………………………13分
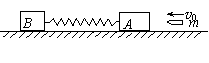 A.动量守恒、机械能守恒
A.动量守恒、机械能守恒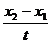 B、
B、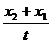
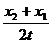 D、
D、
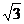 ×108m/s,要使光由玻璃射入空气时折射光线与反射光线成直角,则入射角应是
×108m/s,要使光由玻璃射入空气时折射光线与反射光线成直角,则入射角应是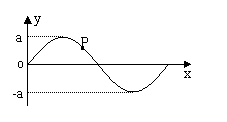 简谐横波某时刻的波形如图示,P为介质中的
简谐横波某时刻的波形如图示,P为介质中的 中,内角A、B、C对边的边长分别是a、b、c,已知c=2,
中,内角A、B、C对边的边长分别是a、b、c,已知c=2,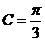
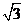 ,求a、b;(2)若sinC+sin(B-A)=2sin2A,求
,求a、b;(2)若sinC+sin(B-A)=2sin2A,求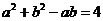 ①
2分
①
2分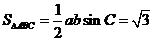 得ab=4
②
4分
得ab=4
②
4分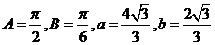 10分
10分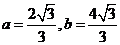
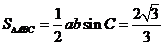 12分
12分 -sinθ,cosθ),θ∈[π,2π].
-sinθ,cosθ),θ∈[π,2π].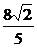 时,求cos(
时,求cos(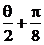 )的值.
)的值.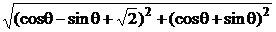
 2分
2分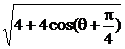
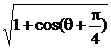 4分
4分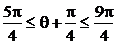 ,∴cos(θ+
,∴cos(θ+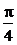 )≤1,|m+n|max=2
)≤1,|m+n|max=2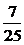 .
8分
.
8分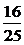 ,
10分
,
10分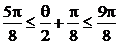 ,∴cos(
,∴cos(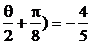 .
12分
.
12分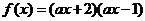 在
在 上存在零点”;
命题
上存在零点”;
命题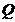 :“只有一个实数满足不等式
:“只有一个实数满足不等式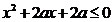 ”,若命题或
”,若命题或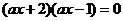 有解
有解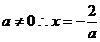 或
或 ……………………………………2分
……………………………………2分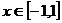 ,故
,故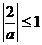 或
或
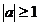 ……………………………………4分
……………………………………4分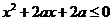 即抛物线
即抛物线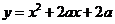 与x轴只有一个交点
与x轴只有一个交点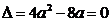
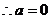 或
或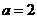 ……………………………………8分
……………………………………8分
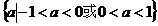 ……………………………………12分
……………………………………12分