(五)、提高选择题与填空题的解题速度
解题的基本原则是“小题不能大做”.解题的基本策略是:巧做.解题的基本方法一
般有:直接求解法,图像法和特殊化法(特殊值法,特殊函数法,特殊角法,特殊数列法,图形特殊位置法,特殊点法,特殊方程法,特殊模型法)等.
考题类型举例:
(1)选择题与填空题
1.(直接法) 是虚数单位,若
是虚数单位,若 ,则
,则 的值是( )
的值是( )
A. B.
B. C.
C. D.
D.
2.(直接法)下列说法错误的是
A. 满足线性回归方程
满足线性回归方程 ;
;
B.“ ”是“
”是“ ”的充分不必要条件;
”的充分不必要条件;
C.在一个 列联表中,由计算得
列联表中,由计算得 ,则其两个变量间有关系的可能性是
,则其两个变量间有关系的可能性是 ;
;
D.命题 ,使得
,使得 的否定
的否定 是
是 ,均有
,均有 。
。
3.(直接法)某地区的一种特色水果上市时间仅能持续几个月,预测上市初期和后期会因供不应求使价格呈连续上涨的态势,而中期又将出现供大于求使价格连续下跌,为准确研究其价格走势,下面给出四个价格模拟函数中适合的是(其中为 常数,
常数, ,且
,且 )
)
A. B.
B.
C. D.
D.
4.(直接法)如果两个位数相同的自然数恰好只有某一数位上的数字不相同,则称这两个数为相邻数.例如:123与103、5555与5565分别是两个相邻数.若集合 中的元素均为两位数,且任意两个数都不是相邻数,则
中的元素均为两位数,且任意两个数都不是相邻数,则 中的元素最多有
中的元素最多有
A.8 个 B.9 个 C.11个 D.12个
5.(代入法)已知等差数列 ,等比数列
,等比数列 ,则该等差数列的公差为( )
,则该等差数列的公差为( )
A. 或
或 B.
B. 或
或 C.
C. D.
D.
6.(图解法)定义在 上的函数
上的函数 是减函数,且函数
是减函数,且函数 的图象关于
的图象关于 成中心对称,若
成中心对称,若 ,
, 满足不等式
满足不等式 .则当
.则当 时,
时, 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
7.(图解法)函数 图像上关于原点对称点共有
图像上关于原点对称点共有
A.0对 B.1对 C.2对 D.3对
8.(特值代验)设 ,那么( )
,那么( )
A. B.
B. C、
C、 D.
D.
9.(特值代验)设 表示不超过
表示不超过 的最大整数(如:
的最大整数(如: ,
, ),则定义在
),则定义在 的
的
函数 的值域为
的值域为
A. B.
B.
C. D.
D. .
.
10.(估值法) 在直角坐标平面上,已知A(-7,0)、B(3,0),点C在直线 上,若∠ACB >
上,若∠ACB > ,则点C的横坐标的取值范围是
,则点C的横坐标的取值范围是
A. B.
B. C.
C. D.
D.
11.(直接法)某单位为了了解用电量y度与气温 之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
|
气温(0C) |
18 |
13 |
10 |
-1 |
|
用电量(度) |
24 |
34 |
38 |
64 |
用线性回归分析,预测当气温为 时,用电量的度数约为 __.(精确到1)
时,用电量的度数约为 __.(精确到1)
12.(直接法)我们可以用随机数法估计 的值,右边程序框图表示其基本步骤
的值,右边程序框图表示其基本步骤
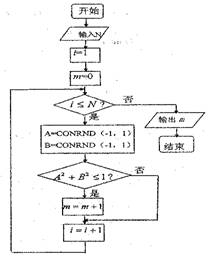 (假设函数
(假设函数 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生
内的任何一个实数).如果输入2000,输出的结果为1572,则由此
可估计 的近似值为
.(保留4位有效数字)
的近似值为
.(保留4位有效数字)
13.(直接法)在 中,角
中,角 所对的边分别为
所对的边分别为 ,
, 表示
表示
 的面积,若
的面积,若 ,
,
则 .
.
14.如果x+x2+x3+……+x9+x10
=a0+a1(1+x)+a2(1+x)2+……+a9(1+x)9+a10(1+x)10,则a9=___ ____.
15.(特例法)已知真命题:过抛物线 的顶点
的顶点 作两条互相垂直的直线,分别交抛物线于另外两点
作两条互相垂直的直线,分别交抛物线于另外两点 ,则直线
,则直线 过定点
过定点 .类比此命题,写出关于椭圆
.类比此命题,写出关于椭圆 的一个真命题:
.
的一个真命题:
.
(2)选考题
坐标系:①已知直线 过点
过点 ,倾斜角为
,倾斜角为 ,定点
,定点 .若直线
.若直线 上的不同两点
上的不同两点 满足
满足 ,求
,求 的值.
的值.
②极坐标系中,求圆 上的点到直线
上的点到直线 距离的取值范围.
距离的取值范围.
不等式:已知 ,又
,又 的最大值为
的最大值为 .
.
(I) 求 的值
的值
(II) 若关于 的不等式
的不等式 有解,求
有解,求 的取值范围.
的取值范围.
(3) 数列:关于某港口今后20年的发展规划,有如下两种方案:
方案甲:按现状进行运营.据测算,每年可收入760万元,但由于港口淤积日益严重,从明年开始需投资进行清淤,第一年投资50万元,以后逐年递增20万元.
方案乙:从明年起开始投资6000万元进行港口改造,以彻底根治港口淤积并提高吞吐能力.港口改造需用时4年,在此期间边改造边运营.据测算,开始改造后港口第一年的收入为320万元,在以后的3年中,每年收入都比上一年增长50%,而后各年的收入都稳定在第4年的水平上.
(I)从明年开始至少经过多少年,方案乙能收回投资(累计总收益为正数)?
(II)从明年开始至少经过多少年,方案乙的累计总收益超过方案甲?(注:收益=收入-投资)
(4) 三角函数:已知 为锐角,且
为锐角,且 .
.
(I)求 的值;
的值;
(II) 求函数 (
( )的最大值和最小值.
)的最大值和最小值.
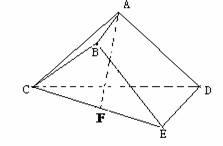
(5) 立体几何
已知多面体 中,
中,
 平面
平面 ,
,
 平面
平面 ,
,
 ,
, .
. ,
, 为
为 的中点.
的中点.
(I)求证: 

 ;
;
(II)求平面 与平面
与平面 所成的锐二面角的大小;
所成的锐二面角的大小;
(III)求多面体 的体积.
的体积.
(6) 概率统计
某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.


(I) 求全班人数及分数在 之间的频数;
之间的频数;
(II) 估计该班的平均分数;
(III) 若要从分数在 之间的试卷中任取4份分析学生失分情况,用
之间的试卷中任取4份分析学生失分情况,用 表示所抽取的试卷中分数在
表示所抽取的试卷中分数在 之间试卷的份数,求
之间试卷的份数,求 的分布列和数学期望.
的分布列和数学期望.
(7)解析几何
(本小题满分13分)如图,已知椭圆 过点
过点 ,且点
,且点 在
在 轴上的射影恰为椭圆的一个焦点.
轴上的射影恰为椭圆的一个焦点.
(I)求椭圆 的方程;
的方程;
(II)在下列两个小题中任选一题作答,若同时选做两题,则只批阅第(ii)小题,第(i)小题的解答,不管正确与否,一律视为无效,不予批阅.
(i)(解答本小题,满分6分)过 作两条倾斜角互补的直线与椭圆分别交于
作两条倾斜角互补的直线与椭圆分别交于 两点.试问:四边形
两点.试问:四边形 能否为平行四边形?若能,求出直线
能否为平行四边形?若能,求出直线 的方程;否则说明理由.
的方程;否则说明理由.
(ii)(解答本小题,满分9分)试问:是否存在斜率为定值的直线 交椭圆于不同的两点
交椭圆于不同的两点 ,使得直线
,使得直线 的倾斜角总是互补?若是,求出直线
的倾斜角总是互补?若是,求出直线 的方程;否则说明理由.
的方程;否则说明理由.
(8) 函数与导数
已知函数 .
.
(I)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(II)若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(III)设函数 ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
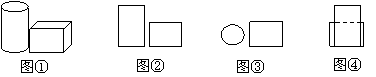
 如图2是某直观图三视图,那么对应的直观图是( ).
如图2是某直观图三视图,那么对应的直观图是( ).