��Ŀ����
3�� ��ͼ��ʾ��ABCDΪ�߳�Ϊ2a�������Σ�OΪ���������ģ�������������ؼ�����ԳƲ��ֱַ���ڷ���ֱABCDƽ��������������ǿ�ų���һ������Ϊ|mؼ�����Ϊq�Ĵ��������Ӵ�B�㴦���ٶ�v��ֱ�ų������������ų������ٶȷ�����BC�н�Ϊ15�㣬����ǡ�þ���O�㣮��֪cos15��=$\frac{\sqrt{6+\sqrt{2}}}{4}$�������������ƣ�
��ͼ��ʾ��ABCDΪ�߳�Ϊ2a�������Σ�OΪ���������ģ�������������ؼ�����ԳƲ��ֱַ���ڷ���ֱABCDƽ��������������ǿ�ų���һ������Ϊ|mؼ�����Ϊq�Ĵ��������Ӵ�B�㴦���ٶ�v��ֱ�ų������������ų������ٶȷ�����BC�н�Ϊ15�㣬����ǡ�þ���O�㣮��֪cos15��=$\frac{\sqrt{6+\sqrt{2}}}{4}$�������������ƣ���1�������ų��ĴŸ�Ӧǿ�ȴ�С��
��2�������Ӵ�CD����������Ҳ�ų��ĴŸ�Ӧǿ���С��ȡֵ��Χ��
���� ��1�����Ӵ�B���������ų����ڴų���������Բ���˶��������˶��켣�����ݼ��ι�ϵ����뾶������������ų��ĴŸ�Ӧǿ�ȴ�С��
��2���Ҳ�ų��Ÿ�Ӧǿ�ȴ�С${B}_{2}^{\;}={B}_{1}^{\;}$ʱ�����Ӵ�D���������Ӧ�ĴŸ�Ӧǿ����С�����˶��켣��CD������ʱ���Ÿ�Ӧǿ������ɼ��ι�ϵ����켣�뾶�����ݰ뾶��ʽ������Ÿ�Ӧǿ�ȣ���������Ÿ�Ӧǿ�ȵķ�Χ��
��� �⣺��1�����Ӵ�B���������ų����˶��켣��ͼ1��ʾ��
$��B{O}_{1}^{\;}O$Ϊ�ȱ������Σ��ɼ��ι�ϵ�ɵù켣�뾶Ϊ��${r}_{1}^{\;}=\sqrt{2}a$
���������ų����˶����У�$qv{B}_{1}^{\;}=m\frac{{v}_{\;}^{2}}{{r}_{1}^{\;}}$
�ã�${B}_{1}^{\;}=\frac{\sqrt{2}mv}{2qa}$
��2�����Ҳ�ų��Ÿ�Ӧǿ�ȴ�С${B}_{2}^{\;}={B}_{1}^{\;}$ʱ�����Ӵ�D����������켣��ͼ2��ʾ���������Ӵ�CD���������С�Ÿ�Ӧǿ��
���Ÿ�Ӧǿ������ʱ���������Ҳ�ų����˶��Ĺ켣�뾶��С�����˶��켣��CD������ʱ���Ÿ�Ӧǿ����켣��ͼ3��ʾ��
�ɼ��ι�ϵ��֪${r}_{2}^{\;}+{r}_{2}^{\;}cos15��=a$
��${r}_{2}^{\;}=\frac{4a}{\sqrt{6}+\sqrt{2}+4}$
�������Ҳ�ų����˶�����$qv{B}_{2m}^{\;}=m\frac{{v}_{\;}^{2}}{{r}_{2}^{\;}}$
��${B}_{2m}^{\;}=\frac{��\sqrt{6}+\sqrt{2}+4��mv}{4qa}$
�����Ӵ�CD��������Ҳ�ų��Ÿ�Ӧǿ�ȴ�С�ķ�ΧΪ
$\frac{\sqrt{2}mv}{2qa}��{B}_{2}^{\;}��\frac{��\sqrt{6}+\sqrt{2}+4��mv}{4qa}$
�𣺣�1�����ų��ĴŸ�Ӧǿ�ȴ�С$\frac{\sqrt{2}mv}{2qa}$��
��2�������Ӵ�CD��������Ҳ�ų��ĴŸ�Ӧǿ���С��ȡֵ��Χ$\frac{\sqrt{2}mv}{2qa}��{B}_{2}^{\;}��\frac{��\sqrt{6}+\sqrt{2}+4��mv}{4qa}$
���� ���������ڴų����˶������ͣ�ȷ����������Դ�������켣������ţ�ٵڶ�������ʽ�ǹ��õĽ���˼·��ƽʱҪ��ǿѵ���������������磮

| A�� | ��һ������������ֲ������仯��������λ�ÿ��ܻᷢ���仯 | |
| B�� | �����ķ���һ����ֱ�ڽӴ��� | |
| C�� | һ�����ֲ����ȵ�ש�飬ƽ�š���ź�����ʱ����������ש�ڵ�λ��һ���仯 | |
| D�� | ֻ�о�ֹ������Ż��ܵ��������� |
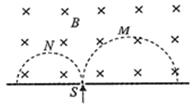 2016��3��10�գ��ҹ���ѧ���������ó�ǿ���̼���ɹ������˷����ʣ��ֽ������ӡ��������Բ�ͬ�����ʾ�С��S��ֱ������ǿ�ų������еİ�Բ�켣��ͼ��������ʾ���������ӵ����������б�����ȷ���ǣ�������
2016��3��10�գ��ҹ���ѧ���������ó�ǿ���̼���ɹ������˷����ʣ��ֽ������ӡ��������Բ�ͬ�����ʾ�С��S��ֱ������ǿ�ų������еİ�Բ�켣��ͼ��������ʾ���������ӵ����������б�����ȷ���ǣ�������| A�� | NΪ�����ӣ�MΪ������ | B�� | N������С��M������ | ||
| C�� | ����������M����������N������ | D�� | M������ʱ�����N������ʱ�� |
 ��ͼ��ʾ���ӳ��ȵĽ���˿Ư���ĵ��ӣ��ٶȿ���Ϊ�㣩�������ٵ糡���ٺ���������м䴹ֱ����ƫת�糡�����ӵ��������ƣ���������������ƫת�糡�������£�������������У�һ����ʹ���ӵ�ƫת�DZ����ǣ�������
��ͼ��ʾ���ӳ��ȵĽ���˿Ư���ĵ��ӣ��ٶȿ���Ϊ�㣩�������ٵ糡���ٺ���������м䴹ֱ����ƫת�糡�����ӵ��������ƣ���������������ƫת�糡�������£�������������У�һ����ʹ���ӵ�ƫת�DZ����ǣ�������| A�� | ��ƫת�糡���ԶԵ� | B�� | ��Сƫת�缫��ľ��� | ||
| C�� | ����ƫת�缫��ĵ�ѹ | D�� | ��Сƫת�缫��ĵ�ѹ |
 ��1�����ⶨ���������ʡ���ʵ���У��ڲ���ש��һ����ֱ��������ͷ��A��B������һ������ֱ��������ͷ��C��D���ڲ�����ĸ���ͷ��Dʱ��Ҫʹ����ס��ͷ��D���ͷ��A��B������ͼ1�ڰ�ֽ�����µ�ʵ��ۼ�������ֱ��a��a��������ֽ�ϵIJ���ש�������ߣ����ݸ�ͼ��ֱ������·ͼ����˵����Ҫ���������������÷��ź�����˵���������i�������r�����ݴ�д������ש�������ʵı���ʽn=$\frac{sini}{sinr}$��
��1�����ⶨ���������ʡ���ʵ���У��ڲ���ש��һ����ֱ��������ͷ��A��B������һ������ֱ��������ͷ��C��D���ڲ�����ĸ���ͷ��Dʱ��Ҫʹ����ס��ͷ��D���ͷ��A��B������ͼ1�ڰ�ֽ�����µ�ʵ��ۼ�������ֱ��a��a��������ֽ�ϵIJ���ש�������ߣ����ݸ�ͼ��ֱ������·ͼ����˵����Ҫ���������������÷��ź�����˵���������i�������r�����ݴ�д������ש�������ʵı���ʽn=$\frac{sini}{sinr}$��


