题目内容
14．
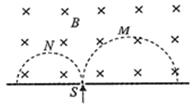2016年3月10日，我国科学家宣布利用超强超短激光成功产生了反物质，现将正电子、负电子以不同的速率经小孔S垂直进入匀强磁场，运行的半圆轨迹如图中虚线所示，不计粒子的重力，下列表述正确的是（ ）| A． | N为负电子，M为正电子 | B． | N的速率小于M的速率 | ||
| C． | 洛伦兹力对M做正功、对N做负功 | D． | M的运行时间大于N的运行时间 |
分析 由左手定则判断出M带正电荷，带负电荷；结合半径的公式可以判断出粒子速度的大小；根据周期的公式可以判断出运动的时间关系．
解答 解：A、由左手定则判断出N带正电荷，M带负电荷，故A错误；
B、粒子在磁场中运动，洛伦兹力提供向心力：evB=m$\frac{{v}^{2}}{r}$，解得：v=$\frac{eBr}{m}$，由图示可知N的轨道半径小于M的轨道半径，则N的速率小于M的速率，故B正确；
C、洛伦兹力始终与粒子的速度垂直，洛伦兹力对粒子不做功，故C错误；
D、正负电子做圆周运动的周期T=$\frac{2πm}{eB}$相同，它们在磁场中的运动时间都是半个周期，它们的运动时间相等，故D错误．
故选：B．
点评 本题考查了电子在磁场中的运动，知道洛伦兹力提供向心力是解题的前提，应用左手定则、牛顿第二定律与粒子做圆周运动的周期公式可以解题．
练习册系列答案
相关题目
4．如图所示，在绝缘粗糙水平面上固定两个等量同种电荷P、Q在PQ连线上的M点由静止释放一带电滑块，则滑块会由静止开始一直向右运动到PQ连线上的另一点N而停下，则以下说法正确的是（ ）
| A． | 滑块受到的电场力可能是先减小后增大 | |
| B． | 滑块的电势能一直减小 | |
| C． | 滑块的动能与电势能之和可能保持不变 | |
| D． | PM间距一定小于QN间距 |
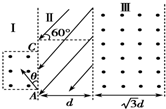如图所示，区域Ⅰ内有一长AC=d的矩形匀强磁场，其磁场方向与区域Ⅲ内的磁场方向相同，均垂直纸面向外，且磁感应强度是区域Ⅲ内磁场磁感应强度的3倍，区域Ⅱ宽为d，其内存在与水平方向成60°角斜向左下的匀强电场，区域Ⅲ宽为$\sqrt{3}$d．一质量为m、带电荷量为q的带正电粒子从A点以初速度v0与边界成θ=30°角垂直磁场方向射入矩形匀强磁场中，并从C点射出而进入匀强电场中，最后粒子恰好垂直区域Ⅲ的右边界从D点（未画出）射出，粒子重力不计，求：
19．
如图所示，匀强磁场分布在平面直角坐标系的整个第I象限内，磁感应强度为B、方向垂直于纸面向里．一质量为m、电荷量绝对值为q、不计重力的粒子，以某速度从O点沿着与y轴夹角为30°的方向进入磁场，运动到A点时，粒子速度沿x轴正方向．下列判断正确的是（ ）
如图所示，匀强磁场分布在平面直角坐标系的整个第I象限内，磁感应强度为B、方向垂直于纸面向里．一质量为m、电荷量绝对值为q、不计重力的粒子，以某速度从O点沿着与y轴夹角为30°的方向进入磁场，运动到A点时，粒子速度沿x轴正方向．下列判断正确的是（ ）| A． | 粒子带正电 | |
| B． | 粒子由O到A经历的时间t=$\frac{πm}{6qB}$ | |
| C． | 若已知A到x轴的距离为d，则粒子速度大小为$\frac{2qBd}{m}$ | |
| D． | 离开第Ⅰ象限时，粒子的速度方向与x轴正方向的夹角为60° |
带电粒子的质量m=1.7×10-27Kg，电量q=1.6×10-19C，以速度v=3.2×106m/s沿垂直于磁场同时又垂直于磁场边界的方向射入匀强磁场中，磁场的磁感应强度为B=0.17T，磁场的宽度L=10cm，如图所示．不计粒子重力．求
如图所示，ABCD为边长为2a的正方形，O为正方形中心，正方形区域左丶右两对称部分分别存在方向垂直ABCD平面向里和向外的匀强磁场．一个质量为|m丶电荷量为q的带正电粒子从B点处以速度v垂直磁场方向射入左侧磁场区域，速度方向与BC边夹角为15°，粒子恰好经过O点．已知cos15°=$\frac{\sqrt{6+\sqrt{2}}}{4}$，粒子重力不计．
4．
带正电的微粒放在电场中，场强的大小和方向随时间变化的规律如图所示．带电微粒只在电场力的作用下由静止开始运动，则下列说法中正确的是（ ）
带正电的微粒放在电场中，场强的大小和方向随时间变化的规律如图所示．带电微粒只在电场力的作用下由静止开始运动，则下列说法中正确的是（ ）| A． | 微粒做往复运动 | |
| B． | 微粒将沿着一条直线运动 | |
| C． | 微粒在第1s内的位移与第3s内的位移相同 | |
| D． | 微粒在0～1s内的加速度与1～2s内的加速度相同 |