题目内容
17.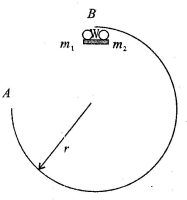 如图所示,一般经为r=0.8m的光滑$\frac{3}{4}$圆轨道AB,A与圆心在同一高度处,在最高点B处有一光滑小托板,上面静止放着两个小球m1=1kg,m2=0.2kg,两球之间压缩着一段弹簧(不与小球连接),初始时刻弹簧被锁定不能弹开.某一时刻,弹簧解锁弹开,m1飞出后恰好落入轨道的A点,m2向右沿轨道运动.弹簧长度和两小球大小均忽略不计,g=10m/s2,求:
如图所示,一般经为r=0.8m的光滑$\frac{3}{4}$圆轨道AB,A与圆心在同一高度处,在最高点B处有一光滑小托板,上面静止放着两个小球m1=1kg,m2=0.2kg,两球之间压缩着一段弹簧(不与小球连接),初始时刻弹簧被锁定不能弹开.某一时刻,弹簧解锁弹开,m1飞出后恰好落入轨道的A点,m2向右沿轨道运动.弹簧长度和两小球大小均忽略不计,g=10m/s2,求:(1)弹簧弹开瞬间m1的速度v1
(2)m2到达轨道最低点时对轨道的压力FN
(3)弹簧被锁定时具有的弹性势能EP.
分析 (1)弹簧弹开m1后,m1做平抛运动,由平抛运动的规律求弹簧弹开瞬间m1的速度v1.
(2)弹簧弹开两个物体的过程,系统的动量守恒,由动量守恒定律求出弹簧弹开瞬间m2的速度v2,对m2,运用机械能守恒定律求出其到达最低点时的速度,再由牛顿运动定律求m2到达轨道最低点时对轨道的压力FN.
(3)根据能量守恒定律求弹簧被锁定时具有的弹性势能EP.
解答 解:(1)弹簧解锁弹开,m1飞出后做平抛运动,则有
r=v1t
r=$\frac{1}{2}g{t}^{2}$
解得 v1=2m/s
(2)弹簧弹开两个物体的过程,取向左为正方向,由动量守恒定律得
m1v1-m2v2=0;
解得 v2=10m/s
对m2,运用机械能守恒定律得
$\frac{1}{2}$m2v22+2m2gr=$\frac{1}{2}{m}_{2}{v}_{3}^{2}$
在最低点,由牛顿第二定律得
FN′-m2g=m2$\frac{{v}_{3}^{2}}{r}$
解得 FN′=35N
根据牛顿第三定律得 FN=FN′=35N
(3)根据能量守恒定律得:
弹簧被锁定时具有的弹性势能 EP=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22=12J
答:
(1)弹簧弹开瞬间m1的速度v1是2m/s.
(2)m2到达轨道最低点时对轨道的压力FN是35N.
(3)弹簧被锁定时具有的弹性势能EP是12J.
点评 分析清楚物体运动过程,把握每个过程的物理规律是正确解题的前提与关键,应用牛顿第二定律、动量守恒定律、能量守恒定律即可正确解题.

练习册系列答案
相关题目
8. 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则下列选项正确的是( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则下列选项正确的是( )
 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则下列选项正确的是( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则下列选项正确的是( )| A. | Ta=Tb=Td=Tc,Ea>Eb=Ed>Ec | |
| B. | Ta=Tb=Td=Tc,Ea=Eb=Ed=Ec | |
| C. | 此过程中棱台对从a点运动的小球做正功 | |
| D. | 此过程中棱台对从d点运动的小球做正功 |
2. 在雷雨天气,避雷针上空出现带电云层时,由于静电感应,避雷针顶部尖端聚集了大量的电荷,避雷针与云层之间的空气就很容易被击穿而成为导体.避雷针就可以把云层上的电荷导入大地,使其不对高层建筑构成危险.如图是某次避雷针放电时,其周围等势线(图中虚线表示)分布图,由图可判断( )
在雷雨天气,避雷针上空出现带电云层时,由于静电感应,避雷针顶部尖端聚集了大量的电荷,避雷针与云层之间的空气就很容易被击穿而成为导体.避雷针就可以把云层上的电荷导入大地,使其不对高层建筑构成危险.如图是某次避雷针放电时,其周围等势线(图中虚线表示)分布图,由图可判断( )
 在雷雨天气,避雷针上空出现带电云层时,由于静电感应,避雷针顶部尖端聚集了大量的电荷,避雷针与云层之间的空气就很容易被击穿而成为导体.避雷针就可以把云层上的电荷导入大地,使其不对高层建筑构成危险.如图是某次避雷针放电时,其周围等势线(图中虚线表示)分布图,由图可判断( )
在雷雨天气,避雷针上空出现带电云层时,由于静电感应,避雷针顶部尖端聚集了大量的电荷,避雷针与云层之间的空气就很容易被击穿而成为导体.避雷针就可以把云层上的电荷导入大地,使其不对高层建筑构成危险.如图是某次避雷针放电时,其周围等势线(图中虚线表示)分布图,由图可判断( )| A. | 避雷针周围的电场方向向下 | |
| B. | 越靠近避雷针尖端电场强度越小 | |
| C. | 越靠近避雷针尖端附近电势变化越快 | |
| D. | 电荷越靠近避雷针尖端,加速度越小 |
9. 如图所示,在有活塞的气缸中密闭着一定质量的理想气体,将一个半导体热敏电阻(阻值随温度的升高而减小)R置于气缸中,气缸固定不动,缸内活塞可以自由移动且不漏气,活塞下挂一沙桶,沙桶装满沙子时活塞恰好能够静止.热敏电阻R与汽缸外的电源E和灵敏电流表A组成闭合回路,气缸和活塞具有良好的绝热性能.如果在沙桶的底部钻上一个小孔,那么在细沙缓缓漏出的过程中,以下判断正确的是( )
如图所示,在有活塞的气缸中密闭着一定质量的理想气体,将一个半导体热敏电阻(阻值随温度的升高而减小)R置于气缸中,气缸固定不动,缸内活塞可以自由移动且不漏气,活塞下挂一沙桶,沙桶装满沙子时活塞恰好能够静止.热敏电阻R与汽缸外的电源E和灵敏电流表A组成闭合回路,气缸和活塞具有良好的绝热性能.如果在沙桶的底部钻上一个小孔,那么在细沙缓缓漏出的过程中,以下判断正确的是( )
 如图所示,在有活塞的气缸中密闭着一定质量的理想气体,将一个半导体热敏电阻(阻值随温度的升高而减小)R置于气缸中,气缸固定不动,缸内活塞可以自由移动且不漏气,活塞下挂一沙桶,沙桶装满沙子时活塞恰好能够静止.热敏电阻R与汽缸外的电源E和灵敏电流表A组成闭合回路,气缸和活塞具有良好的绝热性能.如果在沙桶的底部钻上一个小孔,那么在细沙缓缓漏出的过程中,以下判断正确的是( )
如图所示,在有活塞的气缸中密闭着一定质量的理想气体,将一个半导体热敏电阻(阻值随温度的升高而减小)R置于气缸中,气缸固定不动,缸内活塞可以自由移动且不漏气,活塞下挂一沙桶,沙桶装满沙子时活塞恰好能够静止.热敏电阻R与汽缸外的电源E和灵敏电流表A组成闭合回路,气缸和活塞具有良好的绝热性能.如果在沙桶的底部钻上一个小孔,那么在细沙缓缓漏出的过程中,以下判断正确的是( )| A. | 气体内能将一定增大 | B. | 气体压强将一定减小 | ||
| C. | 气体将一定对外做功 | D. | 电流表的示数将变小 |
8.关于开普勒行星运动定律,下列说法正确的是( )
| A. | 行星运动的方向总是沿椭圆轨道的切线方向 | |
| B. | 行星运动过程中速度大小不变 | |
| C. | 行星运动的方向总是与它和太阳连线垂直 | |
| D. | 太阳系中的行星运动轨道都是圆 |
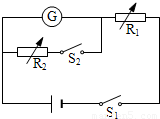 在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材:
在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材: