题目内容
7.2016年3月1日,嫦娥一号卫星系统总指挥兼总设计师叶培建院士表示,中国计划2018年前后发射“嫦娥四号”月球探测器,在月球背面软着陆,假设“嫦娥四号”绕月飞行轨道近似为圆形,距月球表面高度为H,飞行周期为T,月球的半径为R,引力常量为G.求:(1)月球的密度;
(2)月球的表面重力加速度.
分析 (1)先根据万有引力提供向心力求出月球的质量,再根据密度公式求月球的密度
(2)根据重力等于万有引力求出月球表面的重力加速度
解答 解:(1)飞船绕月球做匀速圆周运动,万有引力提供向心力,有
$G\frac{Mm}{(R+h)_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}(R+h)$
解得$M=\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$
月球的密度$ρ=\frac{M}{V}=\frac{\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}}{\frac{4π{R}_{\;}^{3}}{3}}$=$\frac{3π(R+h)_{\;}^{3}}{G{T}_{\;}^{2}{R}_{\;}^{3}}$
(2)根据月球表面物体重力等于万有引力
$mg=G\frac{Mm}{{R}_{\;}^{2}}$
解得:$g=\frac{GM}{{R}_{\;}^{2}}$=$\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{{R}_{\;}^{2}{T}_{\;}^{2}}$
答:(1)月球的密度$\frac{3π(R+h)_{\;}^{3}}{G{T}_{\;}^{2}{R}_{\;}^{3}}$;
(2)月球的表面重力加速度$\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{{R}_{\;}^{2}{T}_{\;}^{2}}$.
点评 本题关键是要知道飞船绕月球做圆周运动的向心力由万有引力提供,并且要能够根据题目的要求选择恰当的向心力的表达式,同时知道在月球表面物体重力等于万有引力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图所示,质量不计的光滑直杆AB的A端固定一个小球P,杆OB段套着小球Q,Q与轻质弹簧的一端相连,弹簧的另一端固定在O点,弹簧原长为50cm,劲度系数为K=76.4N/m,两球的质量均为m=0.1kg,OA=1m,小球半径忽略.现使直杆在竖直平面内绕过O点的水平轴匀速转动,转速大小为$\frac{360}{π}$r/min,若OB段足够长,弹性形变始终处于弹性限度内,g=10m/s2,则( )
如图所示,质量不计的光滑直杆AB的A端固定一个小球P,杆OB段套着小球Q,Q与轻质弹簧的一端相连,弹簧的另一端固定在O点,弹簧原长为50cm,劲度系数为K=76.4N/m,两球的质量均为m=0.1kg,OA=1m,小球半径忽略.现使直杆在竖直平面内绕过O点的水平轴匀速转动,转速大小为$\frac{360}{π}$r/min,若OB段足够长,弹性形变始终处于弹性限度内,g=10m/s2,则( )
 如图所示,质量不计的光滑直杆AB的A端固定一个小球P,杆OB段套着小球Q,Q与轻质弹簧的一端相连,弹簧的另一端固定在O点,弹簧原长为50cm,劲度系数为K=76.4N/m,两球的质量均为m=0.1kg,OA=1m,小球半径忽略.现使直杆在竖直平面内绕过O点的水平轴匀速转动,转速大小为$\frac{360}{π}$r/min,若OB段足够长,弹性形变始终处于弹性限度内,g=10m/s2,则( )
如图所示,质量不计的光滑直杆AB的A端固定一个小球P,杆OB段套着小球Q,Q与轻质弹簧的一端相连,弹簧的另一端固定在O点,弹簧原长为50cm,劲度系数为K=76.4N/m,两球的质量均为m=0.1kg,OA=1m,小球半径忽略.现使直杆在竖直平面内绕过O点的水平轴匀速转动,转速大小为$\frac{360}{π}$r/min,若OB段足够长,弹性形变始终处于弹性限度内,g=10m/s2,则( )| A. | 当球P转到最高点时,球P对杆有向上的作用力 | |
| B. | 小球Q的线速度大小为6m/s | |
| C. | 当直杆转到与水平方向平行时,弹簧对小球Q的弹力约为8.87N | |
| D. | 当球Q转到最高点时,弹簧的形变量大小为12cm |
19.关于光的波粒二象性,下列理解正确的是( )
| A. | 当光子静止时有粒子性,光子传播时有波动性 | |
| B. | 光是一种宏观粒子,但它按波的方式传播 | |
| C. | 光子在空间各点出现的可能性大小(概率)可以用波动规律来描述 | |
| D. | 大量光子出现的时候表现出波动性,个别光子出现的时候表现出粒子性 | |
| E. | 不仅光具有波粒二象性,微观粒子也具有波粒二象性 |
12.下列说法正确的是( )
| A. | ${\;}_{6}^{14}C$经一次α衰变后成为${\;}_{7}^{14}C$ | |
| B. | ${\;}_{2}^{4}$He核由两个中子和两个质子组成 | |
| C. | 核反应方程应遵循质子数和中子数守恒 | |
| D. | 温度升高不能改变放射性元素的半衰期 |
19. 用两条细绳分别系住两小球A、B如图所示.绳OA的长度是绳O′B的两倍,A球的质量是B球的两倍.将两球从水平位置由静止释放,以初始水平面为参考面,则( )
用两条细绳分别系住两小球A、B如图所示.绳OA的长度是绳O′B的两倍,A球的质量是B球的两倍.将两球从水平位置由静止释放,以初始水平面为参考面,则( )
 用两条细绳分别系住两小球A、B如图所示.绳OA的长度是绳O′B的两倍,A球的质量是B球的两倍.将两球从水平位置由静止释放,以初始水平面为参考面,则( )
用两条细绳分别系住两小球A、B如图所示.绳OA的长度是绳O′B的两倍,A球的质量是B球的两倍.将两球从水平位置由静止释放,以初始水平面为参考面,则( )| A. | A、B两球到达最低点时加速度相等 | |
| B. | A、B两球到达最低点时机械能相等 | |
| C. | A、B两球到达最低点时机械能不相等 | |
| D. | A、B两球在最低点时对绳的拉力相等 |
16.关于万有引力定律,下列说法中正确的是( )
| A. | 万有引力定律是牛顿在总结前人研究成果的基础上发现的 | |
| B. | 万有引力定律适宜于质点间的相互作用 | |
| C. | 公式中的G是一个比例常数,是有单位的,单位是N•m2/kg2 | |
| D. | 任何两个质量分布均匀的球体之间的相互作用可以用该公式来计算,r是两球球心之间的距离 |
 如图所示,质量为m=1kg、横截面为直角三角形的物块ABC,∠ABC=37°,AB靠在墙壁上,动摩擦因数为0.5,F是垂直于斜面BC的推力,在此推力作用下,物体以加速度a=5m/s2在竖直方向上做匀加速直线运动.(sin37°=0.6,cos37°=0.8,g取10m/s2).求:推力F的大小可能为多大?
如图所示,质量为m=1kg、横截面为直角三角形的物块ABC,∠ABC=37°,AB靠在墙壁上,动摩擦因数为0.5,F是垂直于斜面BC的推力,在此推力作用下,物体以加速度a=5m/s2在竖直方向上做匀加速直线运动.(sin37°=0.6,cos37°=0.8,g取10m/s2).求:推力F的大小可能为多大?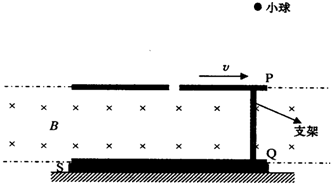
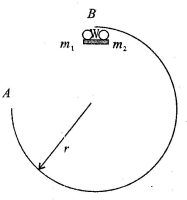 如图所示,一般经为r=0.8m的光滑$\frac{3}{4}$圆轨道AB,A与圆心在同一高度处,在最高点B处有一光滑小托板,上面静止放着两个小球m1=1kg,m2=0.2kg,两球之间压缩着一段弹簧(不与小球连接),初始时刻弹簧被锁定不能弹开.某一时刻,弹簧解锁弹开,m1飞出后恰好落入轨道的A点,m2向右沿轨道运动.弹簧长度和两小球大小均忽略不计,g=10m/s2,求:
如图所示,一般经为r=0.8m的光滑$\frac{3}{4}$圆轨道AB,A与圆心在同一高度处,在最高点B处有一光滑小托板,上面静止放着两个小球m1=1kg,m2=0.2kg,两球之间压缩着一段弹簧(不与小球连接),初始时刻弹簧被锁定不能弹开.某一时刻,弹簧解锁弹开,m1飞出后恰好落入轨道的A点,m2向右沿轨道运动.弹簧长度和两小球大小均忽略不计,g=10m/s2,求: