题目内容
9. 如图所示,固定光滑斜面体倾角为37°,CDE为竖直面内的光滑圆弧轨道,一小球从斜面的底端A点,以初速度v0=4$\sqrt{3}$m/s沿斜面向上滚动,离开斜面体后刚好从圆弧轨道的C点无碰撞地进人圆弧轨道,已知斜面顶点B比C点高h=0.152m,斜面的长为L=1m,小球的质量为1kg,g取10m/s2,$\sqrt{61}$=7.81,求:
如图所示,固定光滑斜面体倾角为37°,CDE为竖直面内的光滑圆弧轨道,一小球从斜面的底端A点,以初速度v0=4$\sqrt{3}$m/s沿斜面向上滚动,离开斜面体后刚好从圆弧轨道的C点无碰撞地进人圆弧轨道,已知斜面顶点B比C点高h=0.152m,斜面的长为L=1m,小球的质量为1kg,g取10m/s2,$\sqrt{61}$=7.81,求:(1)圆弧轨道的半径;
(2)试分析小球进入圆弧轨道后恰好能运动到与圆弧圆心0等高处,则小球在圆弧轨道内克服摩擦力做功为多少?
分析 (1)小球从A到B做匀减速运动,从B到C做斜抛运动,分别由动能定理求出B点和C点的速度,将B点速度分解求出水平速度,在C点利用速度的分解和几何关系联立可求圆弧轨道的半径;
(2)因为在C点无机械能损失,所以全过程用动能定理可求小球在圆弧轨道内克服摩擦力做的功.
解答 解:(1)从A到B,由动能定理可得:-mgLsin37°=$\frac{1}{2}$m${v}_{B}^{2}$-$\frac{1}{2}$m${v}_{0}^{2}$ ①
物体经过B点飞出后做斜抛运动,其水平速度为:vx=vBcos37° ②
从A到C,由动能定理可得:-mg(Lsin37°-h)=$\frac{1}{2}$m${v}_{c}^{2}$-$\frac{1}{2}$m${v}_{0}^{2}$ ③
设∠COD的夹角为θ,在C点将速度vC分解可得:cosθ=$\frac{{v}_{x}}{{v}_{c}}$ ④
又由几何关系有:(Lsin37°-h)=R(1-cosθ) ⑤
联立①②③④⑤解得:R=1.93m. ⑥
(2)小球进入圆弧轨道后恰好能运动到与圆弧圆心0等高处,即在等高处的速度为0,因为在C点无机械能损失,所以对全过程:
由动能定理可得:-mgR-Wf=0-$\frac{1}{2}$mv02 ⑦
代入数据解得:Wf=4.7J ⑧
答:(1)圆弧轨道的半径为1.93m;
(2)小球在圆弧轨道内克服摩擦力做功为4.7J.
点评 本题考查动能定理、斜抛运动和圆周运动等知识的综合运用,解答此题时要认真分析物体的运动过程,使用动能定理是可以全过程,也可以分过程,还要注意题干给定的条件:“离开斜面体后刚好从圆弧轨道的C点无碰撞地进人圆弧轨道”、“小球进入圆弧轨道后恰好能运动到与圆弧圆心0等高处”的含义.

 如图,S1、S2是振幅均为A的两个水波波源,某时刻它们形成的波峰和波谷分别由实线和虚线表示.则( )
如图,S1、S2是振幅均为A的两个水波波源,某时刻它们形成的波峰和波谷分别由实线和虚线表示.则( )| A. | 两列波在相遇区域发生干涉 | |
| B. | a处质点振动始终减弱,b、c处质点振动始终加强 | |
| C. | 此时a、b、c处各质点的位移是:xa=0,xb=-2A,xc=2A | |
| D. | a、b、c处各质点随着水波飘向远处 |
| A. | “用油膜法估测分子的大小”实验中油酸分子直径等于纯油酸体积除以相应油酸膜的面积 | |
| B. | 理想气体在体积不变的情况下,压强p与热力学温度T成正比 | |
| C. | 气体分子的平均动能越大,气体的压强就越大 | |
| D. | 两个分子甲和乙相距较远(此时它们之间的作用力可以忽略),设甲固定不动,乙逐渐向甲靠近,直到不能再靠近,在整个移动过程中前阶段分子力做正功,后阶段克服分子力做功 | |
| E. | 液体的表面张力是由于液体分子间的相互作用引起的 |
 如图所示,一竖直平面内有OA、OB、OC三个倾角不同的斜面,它们的底端都相交于O点,竖直的虚线圆与水平面相切于O点,虚线PQ水平,虚线MN竖直.现将一系列完全相同的滑块(可视为质点)分别从这些斜面上的某点同时由静止释放,系列判断正确的是( )
如图所示,一竖直平面内有OA、OB、OC三个倾角不同的斜面,它们的底端都相交于O点,竖直的虚线圆与水平面相切于O点,虚线PQ水平,虚线MN竖直.现将一系列完全相同的滑块(可视为质点)分别从这些斜面上的某点同时由静止释放,系列判断正确的是( )| A. | 若各斜面均光滑,滑块释放时分别处在同一水平虚线PQ与各斜面的交点上,则这些滑块到达O点的速率相等 | |
| B. | 若各斜面均光滑,滑块释放时分别处在虚线圆与各斜面的交点上,则这些滑块到达O点的时间相等 | |
| C. | 若各斜面均光滑,滑块释放时分别处在同一水平虚线PQ与各斜面的交点上,则这些滑块到达O点时的重力的瞬时功率相等 | |
| D. | 若各斜面与这些滑块间的动摩擦因数相等,滑块释放时分别处于同一竖直虚线MN与各斜面的交点上,则滑到O点的过程中,各滑块损失的机械能相等 |
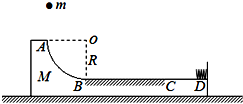 如图所示,竖直平面内轨道ABCD的质量M=0.4kg,放在光滑水平面上,其中AB段是半径为R=0.4m的光滑四分之一圆弧,在B点与水平轨道BD相切,水平轨道的BC段粗糙,动摩擦因数μ=0.4,长L=3.5m,CD段光滑,D端连一轻弹簧,现有一质量m=0.1kg的小物体(可视为质点)在距A点高为H=3.6m处由静止自由落下,恰沿A点滑入圆弧轨道(g=10m/s2),求:
如图所示,竖直平面内轨道ABCD的质量M=0.4kg,放在光滑水平面上,其中AB段是半径为R=0.4m的光滑四分之一圆弧,在B点与水平轨道BD相切,水平轨道的BC段粗糙,动摩擦因数μ=0.4,长L=3.5m,CD段光滑,D端连一轻弹簧,现有一质量m=0.1kg的小物体(可视为质点)在距A点高为H=3.6m处由静止自由落下,恰沿A点滑入圆弧轨道(g=10m/s2),求:
 如图所示,质量m=0.2kg的小球从某高度处以初速度v0=4m/s水平抛出,之后恰好沿着斜面方向落在倾角为37°的光滑斜面上,并沿着斜面下滑至地面,已知小球在斜面上下滑的时间为0.2s,不计空气阻力,取水平地面为重力势能的参考平面,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,质量m=0.2kg的小球从某高度处以初速度v0=4m/s水平抛出,之后恰好沿着斜面方向落在倾角为37°的光滑斜面上,并沿着斜面下滑至地面,已知小球在斜面上下滑的时间为0.2s,不计空气阻力,取水平地面为重力势能的参考平面,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求: 如图,U型玻璃细管竖直放置,足够长水平细管又与U型玻璃细管底部相连通,各部分细管内径相同.水平细管内用小活塞封有长度为10cm的理想气体A,U型管左管上端封有长度为10cm的理想气体B,右管上端开口并与大气相通.此时U型玻璃管左右两侧水银面恰好相平,水银面距U型玻璃管底部的高度为15cm.现将活塞缓慢向左拉,使气体B的长度变为11cm.已知外界大气压强为75cmHg.求:
如图,U型玻璃细管竖直放置,足够长水平细管又与U型玻璃细管底部相连通,各部分细管内径相同.水平细管内用小活塞封有长度为10cm的理想气体A,U型管左管上端封有长度为10cm的理想气体B,右管上端开口并与大气相通.此时U型玻璃管左右两侧水银面恰好相平,水银面距U型玻璃管底部的高度为15cm.现将活塞缓慢向左拉,使气体B的长度变为11cm.已知外界大气压强为75cmHg.求: 如图所示,半径R=0.4m的光滑圆弧轨道BC固定在竖直平面内,轨道的上端点B和圆心O的连线与水平方向的夹角θ=30°,下端点C为轨道的最低点且与水平面相切,质量m=0.1kg的小物块(可视为质点)从空中的A点以v0=2m/s的速度被水平抛出,恰好从B点沿轨道切线方向进人轨道,经过C点后沿水平面向右运动,g取10m/s.求:
如图所示,半径R=0.4m的光滑圆弧轨道BC固定在竖直平面内,轨道的上端点B和圆心O的连线与水平方向的夹角θ=30°,下端点C为轨道的最低点且与水平面相切,质量m=0.1kg的小物块(可视为质点)从空中的A点以v0=2m/s的速度被水平抛出,恰好从B点沿轨道切线方向进人轨道,经过C点后沿水平面向右运动,g取10m/s.求: