题目内容
19. 质量为m的小球系在轻杆一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力作用.某时刻,小球通过轨道最低点,轻杆对球的拉力大小为7mg,此后小球做圆周运动,经过半周到达最高点时,杆对球的作用力大小为$\frac{1}{2}$mg,则在这半周中小球克服空气阻力所做的功可能是( )
质量为m的小球系在轻杆一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力作用.某时刻,小球通过轨道最低点,轻杆对球的拉力大小为7mg,此后小球做圆周运动,经过半周到达最高点时,杆对球的作用力大小为$\frac{1}{2}$mg,则在这半周中小球克服空气阻力所做的功可能是( )| A. | $\frac{1}{4}$mgR | B. | $\frac{1}{2}$mgR | C. | $\frac{3}{4}$mgR | D. | mgR |
分析 根据杆对球的作用力,通过牛顿第二定律求得求得速度,然后对球从最低点到最高点的运动过程应用动能定理即可求解.
解答 解:在最低点,竖直方向上小球的合外力做向心力,方向向上,故轻杆对球的拉力方向向上,小球的向心力为:
${F}_{1}=\frac{m{{v}_{1}}^{2}}{R}=7mg-mg=6mg$;
在最高点,竖直方向上小球的合外力做向心力,方向向下,故若杆对球的作用力向下,那么向心力为:${F}_{2}=\frac{m{{v}_{2}}^{2}}{R}=\frac{3}{2}mg$
若杆对球的作用力向上,那么向心力为:${F}_{2}'=\frac{m{{v}_{2}}'^{2}}{R}=\frac{1}{2}mg$;
那么对小球从最低点运动到最高点的过程中,杆对球的作用力与速度方向垂直,不做功,故只有重力和阻力做功,故由动能定理可得这半周中小球克服空气阻力所做的功为:
$W=\frac{1}{2}m{{v}_{1}}^{2}-\frac{1}{2}m{{v}_{2}}^{2}-2mgR=\frac{1}{4}mgR$
或为:$W'=\frac{1}{2}m{{v}_{1}}^{2}-\frac{1}{2}m{{v}_{2}}'^{2}-2mgR=\frac{3}{4}mgR$
故AC正确,BD错误;
故选:AC.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
9.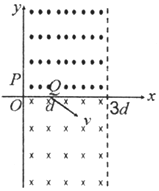 如图所示,在区域I(0≤x≤3d,y>0)内存在着垂直xOy平面向外的匀强磁场,磁感应强度大小为2B,在区域Ⅱ(0≤x≤3d,y<0)内存在着垂直xOy平面向里的匀强磁场,磁感应强度大小为B.质量为m、带电量为q(q>0)的a、b两个粒子同时从y轴上的P点沿x轴正向以不同速率进入区域I.已知某时刻a粒子从Q点(d,0)进入区域Ⅱ时,速度方向与x轴正向的夹角为30°(如图).不计粒子的重力和粒子间的相互作用,下列说法正确的是( )
如图所示,在区域I(0≤x≤3d,y>0)内存在着垂直xOy平面向外的匀强磁场,磁感应强度大小为2B,在区域Ⅱ(0≤x≤3d,y<0)内存在着垂直xOy平面向里的匀强磁场,磁感应强度大小为B.质量为m、带电量为q(q>0)的a、b两个粒子同时从y轴上的P点沿x轴正向以不同速率进入区域I.已知某时刻a粒子从Q点(d,0)进入区域Ⅱ时,速度方向与x轴正向的夹角为30°(如图).不计粒子的重力和粒子间的相互作用,下列说法正确的是( )
 如图所示,在区域I(0≤x≤3d,y>0)内存在着垂直xOy平面向外的匀强磁场,磁感应强度大小为2B,在区域Ⅱ(0≤x≤3d,y<0)内存在着垂直xOy平面向里的匀强磁场,磁感应强度大小为B.质量为m、带电量为q(q>0)的a、b两个粒子同时从y轴上的P点沿x轴正向以不同速率进入区域I.已知某时刻a粒子从Q点(d,0)进入区域Ⅱ时,速度方向与x轴正向的夹角为30°(如图).不计粒子的重力和粒子间的相互作用,下列说法正确的是( )
如图所示,在区域I(0≤x≤3d,y>0)内存在着垂直xOy平面向外的匀强磁场,磁感应强度大小为2B,在区域Ⅱ(0≤x≤3d,y<0)内存在着垂直xOy平面向里的匀强磁场,磁感应强度大小为B.质量为m、带电量为q(q>0)的a、b两个粒子同时从y轴上的P点沿x轴正向以不同速率进入区域I.已知某时刻a粒子从Q点(d,0)进入区域Ⅱ时,速度方向与x轴正向的夹角为30°(如图).不计粒子的重力和粒子间的相互作用,下列说法正确的是( )| A. | a粒子在区域I中做圆周运动的半径大小为d | |
| B. | a粒子离开区域Ⅱ时的速度方向沿y 轴正方向 | |
| C. | a粒子在区域I和区域Ⅱ中运动的总时间为$\frac{πm}{4qB}$ | |
| D. | a、b两个粒子一定同时离开磁场 |
4.以下说法中正确的是( )
| A. | 增透膜是利用了光的色散现象 | |
| B. | 电子表的液晶显示是利用了光的偏振现象 | |
| C. | 照相机镜头在阳光下呈现淡紫色是光的全发射现象 | |
| D. | 电视机遥控器是利用发出红外线脉冲信号来变换频道的 | |
| E. | 声波击碎玻璃杯的实验原理是共振 |
11.下列说法符合事实的是( )
| A. | 光电效应说明了光具有波动性 | |
| B. | 查德威克用α粒子轰击氮14获得反冲核氧18,发现了中子 | |
| C. | 贝克勒尔发现的天然放射性现象,说明原子核有复杂结构 | |
| D. | 汤姆生通过对阴极射线的研究,提出了原子核式结构模型 |
8.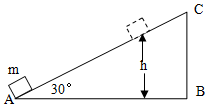 如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{2}{3}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{2}{3}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
 如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{2}{3}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{2}{3}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了mgh | B. | 动能损失了$\frac{4}{3}$mgh | ||
| C. | 克服摩擦力做功$\frac{1}{6}$mgh | D. | 机械能损失了$\frac{1}{2}$mgh |
9. 如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ.当小球以某一角速度匀速转动时,恰好对锥面无压力,则下列说法正确的是( )
如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ.当小球以某一角速度匀速转动时,恰好对锥面无压力,则下列说法正确的是( )
 如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ.当小球以某一角速度匀速转动时,恰好对锥面无压力,则下列说法正确的是( )
如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ.当小球以某一角速度匀速转动时,恰好对锥面无压力,则下列说法正确的是( )| A. | 小球运动的角速度大小是$\sqrt{\frac{g}{Lcosθ}}$ | B. | 小球运动的角速度大小是$\sqrt{\frac{gtanθ}{L}}$ | ||
| C. | 细线的拉力大小是$\frac{mg}{sinθ}$ | D. | 细线的拉力大小是$\frac{mg}{cosθ}$ |
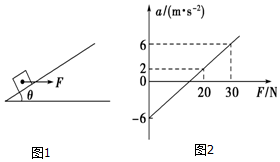 如图1所示,用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图2示,若重力加速度g取10m/s2,根据图中所提供的信息求解
如图1所示,用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图2示,若重力加速度g取10m/s2,根据图中所提供的信息求解 两轮平衡车(如图所示)广受年轻人的喜爱.它的动力系统由电池驱动,能够输出的最大功率为P0.小明驾驶平衡车在水平路面上沿直线运动时,受到的阻力恒为f,已知小明和平衡车的总质量为m,在以下讨论中,忽略小明身体姿态调整引起的重心位置的变化,并忽略小明对系统做的功.
两轮平衡车(如图所示)广受年轻人的喜爱.它的动力系统由电池驱动,能够输出的最大功率为P0.小明驾驶平衡车在水平路面上沿直线运动时,受到的阻力恒为f,已知小明和平衡车的总质量为m,在以下讨论中,忽略小明身体姿态调整引起的重心位置的变化,并忽略小明对系统做的功. 如图所示,一轻弹簧原长为2R,其一端固定在倾角为370的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然状态,直轨道与一半径为$\frac{5}{6}$R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直平面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高到达F点,AF=4R,已知P与直轨道间的动摩擦因数?=$\frac{1}{4}$,重力加速度为g,sin37°=0.6,cos37°=0.8.则:
如图所示,一轻弹簧原长为2R,其一端固定在倾角为370的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然状态,直轨道与一半径为$\frac{5}{6}$R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直平面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高到达F点,AF=4R,已知P与直轨道间的动摩擦因数?=$\frac{1}{4}$,重力加速度为g,sin37°=0.6,cos37°=0.8.则: