题目内容
9.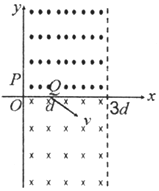 如图所示,在区域I(0≤x≤3d,y>0)内存在着垂直xOy平面向外的匀强磁场,磁感应强度大小为2B,在区域Ⅱ(0≤x≤3d,y<0)内存在着垂直xOy平面向里的匀强磁场,磁感应强度大小为B.质量为m、带电量为q(q>0)的a、b两个粒子同时从y轴上的P点沿x轴正向以不同速率进入区域I.已知某时刻a粒子从Q点(d,0)进入区域Ⅱ时,速度方向与x轴正向的夹角为30°(如图).不计粒子的重力和粒子间的相互作用,下列说法正确的是( )
如图所示,在区域I(0≤x≤3d,y>0)内存在着垂直xOy平面向外的匀强磁场,磁感应强度大小为2B,在区域Ⅱ(0≤x≤3d,y<0)内存在着垂直xOy平面向里的匀强磁场,磁感应强度大小为B.质量为m、带电量为q(q>0)的a、b两个粒子同时从y轴上的P点沿x轴正向以不同速率进入区域I.已知某时刻a粒子从Q点(d,0)进入区域Ⅱ时,速度方向与x轴正向的夹角为30°(如图).不计粒子的重力和粒子间的相互作用,下列说法正确的是( )| A. | a粒子在区域I中做圆周运动的半径大小为d | |
| B. | a粒子离开区域Ⅱ时的速度方向沿y 轴正方向 | |
| C. | a粒子在区域I和区域Ⅱ中运动的总时间为$\frac{πm}{4qB}$ | |
| D. | a、b两个粒子一定同时离开磁场 |
分析 根据几何关系求出a粒子在区域I中做圆周运动的半径,从而根据半径公式得出在区域Ⅱ中的半径,作出轨迹,根据几何关系求出在两个磁场中的圆心角,求出运动的总时间.
解答 解:A、根据几何关系知,a粒子在区域I中做圆周运动的半径大小r=2d,故A错误.
B、根据r=$\frac{mv}{qB}$知,a粒子进入区域Ⅱ时的速度大小不变,磁感应强度变为原来的一半,则半径变为原来的2倍,可知a粒子在区域Ⅱ中的轨道半径r′=4d,根据几何关系知,粒子a离开区域Ⅱ时速度方向沿x轴正方向,故B错误.
C、根据几何关系知,粒子a在区域I和区域Ⅱ中做圆周运动的圆心角均为30°,则a粒子在区域I和区域Ⅱ中运动的总时间t=$\frac{1}{12}×\frac{2πm}{2qB}+\frac{1}{12}×\frac{2πm}{qB}=\frac{πm}{4qB}$,故C正确.
D、a、b两粒子的速度不同,在磁场中做圆周运动的圆心角不同,周期相同,则运动时间不同,所以a、b两粒子不能同时离开磁场,故D错误.
故选:C.
点评 本题考查了带电粒子在磁场中的运动,关键作出粒子运动的轨迹图,结合几何关系和半径公式、周期公式进行求解.

练习册系列答案
相关题目
20. 如图所示,是汞原子的能级图,一个自由电子的总能量为8.0ev,与处于基态的汞原子碰撞后(不计汞原子的动量变化),则电子剩余的能量可能为(碰撞无能量损失)( )
如图所示,是汞原子的能级图,一个自由电子的总能量为8.0ev,与处于基态的汞原子碰撞后(不计汞原子的动量变化),则电子剩余的能量可能为(碰撞无能量损失)( )
 如图所示,是汞原子的能级图,一个自由电子的总能量为8.0ev,与处于基态的汞原子碰撞后(不计汞原子的动量变化),则电子剩余的能量可能为(碰撞无能量损失)( )
如图所示,是汞原子的能级图,一个自由电子的总能量为8.0ev,与处于基态的汞原子碰撞后(不计汞原子的动量变化),则电子剩余的能量可能为(碰撞无能量损失)( )| A. | 0.3ev | B. | 3.1ev | C. | 4.9ev | D. | 8.8ev |
4.下列说法正确的是( )
| A. | 单晶体和多晶体在物理性质上都表现出各向异性 | |
| B. | 液体表面张力产生的原因是表面层分子较稀疏,分子间引力小于斥力 | |
| C. | 液晶显示器利用了液晶对光具有各向异性的特点 | |
| D. | 玻璃没有固定的熔点,但有规则的几何形状,所以是晶体 |
14.下列说法中不正确的是( )
| A. | 电动机是把其他形式的能转化为电能的装置 | |
| B. | 发电机是把其他形式的能转化为电能的装置 | |
| C. | 电容器是储存电荷的装置 | |
| D. | 远距离输电一定要用高压输电 |
1. 2017年4月18日,在全国男子举重锦标赛暨第十三届全运会预赛94公斤级比赛中,广西选手李兵以抓举161kg、挺举213kg,总成绩374kg夺得挺举、总成绩两项冠军.如图是李兵的第三把挺举,则在杠铃被举升高的过程中,下列说法正确的是( )
2017年4月18日,在全国男子举重锦标赛暨第十三届全运会预赛94公斤级比赛中,广西选手李兵以抓举161kg、挺举213kg,总成绩374kg夺得挺举、总成绩两项冠军.如图是李兵的第三把挺举,则在杠铃被举升高的过程中,下列说法正确的是( )
 2017年4月18日,在全国男子举重锦标赛暨第十三届全运会预赛94公斤级比赛中,广西选手李兵以抓举161kg、挺举213kg,总成绩374kg夺得挺举、总成绩两项冠军.如图是李兵的第三把挺举,则在杠铃被举升高的过程中,下列说法正确的是( )
2017年4月18日,在全国男子举重锦标赛暨第十三届全运会预赛94公斤级比赛中,广西选手李兵以抓举161kg、挺举213kg,总成绩374kg夺得挺举、总成绩两项冠军.如图是李兵的第三把挺举,则在杠铃被举升高的过程中,下列说法正确的是( )| A. | 杠铃的动能一直增加 | |
| B. | 杠铃和地球组成系统的重力势能一直增加 | |
| C. | 运动员对杠铃一直做正功 | |
| D. | 运动员对杠铃先做正功后做负功 |
19. 质量为m的小球系在轻杆一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力作用.某时刻,小球通过轨道最低点,轻杆对球的拉力大小为7mg,此后小球做圆周运动,经过半周到达最高点时,杆对球的作用力大小为$\frac{1}{2}$mg,则在这半周中小球克服空气阻力所做的功可能是( )
质量为m的小球系在轻杆一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力作用.某时刻,小球通过轨道最低点,轻杆对球的拉力大小为7mg,此后小球做圆周运动,经过半周到达最高点时,杆对球的作用力大小为$\frac{1}{2}$mg,则在这半周中小球克服空气阻力所做的功可能是( )
 质量为m的小球系在轻杆一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力作用.某时刻,小球通过轨道最低点,轻杆对球的拉力大小为7mg,此后小球做圆周运动,经过半周到达最高点时,杆对球的作用力大小为$\frac{1}{2}$mg,则在这半周中小球克服空气阻力所做的功可能是( )
质量为m的小球系在轻杆一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力作用.某时刻,小球通过轨道最低点,轻杆对球的拉力大小为7mg,此后小球做圆周运动,经过半周到达最高点时,杆对球的作用力大小为$\frac{1}{2}$mg,则在这半周中小球克服空气阻力所做的功可能是( )| A. | $\frac{1}{4}$mgR | B. | $\frac{1}{2}$mgR | C. | $\frac{3}{4}$mgR | D. | mgR |