题目内容
18.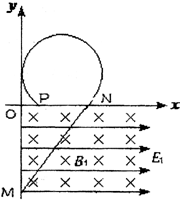 如图所示,在x轴下方存在着正交的电场与磁场,电场方向沿x轴正方向,电场强度大小为E1,磁场方向垂直纸面向里,磁感应强度大小为B1.一个质量m=3g,电荷量q=2×10-3 C的带正电小球自y轴上的M点沿直线匀速运动到x轴上的N点,速度大小v=5 m/s,方向与水平方向成θ=53°角,且已知OM=4 m.在x轴上方存在正交的匀强电场E2与匀强磁场B2(图中均未画出),小球在x轴上方做圆周运动,恰好与y轴相切,运动轨迹如图所示.(g=10 m/s2,sin53°=0.8)求:
如图所示,在x轴下方存在着正交的电场与磁场,电场方向沿x轴正方向,电场强度大小为E1,磁场方向垂直纸面向里,磁感应强度大小为B1.一个质量m=3g,电荷量q=2×10-3 C的带正电小球自y轴上的M点沿直线匀速运动到x轴上的N点,速度大小v=5 m/s,方向与水平方向成θ=53°角,且已知OM=4 m.在x轴上方存在正交的匀强电场E2与匀强磁场B2(图中均未画出),小球在x轴上方做圆周运动,恰好与y轴相切,运动轨迹如图所示.(g=10 m/s2,sin53°=0.8)求:(1)求电场强度E1和磁感应强度B1的大小;
(2)电场E2的大小与方向;
(3)磁场B2的大小与方向.
分析 (1)根据小球的运动可知小球受力平衡,合外力为零;对小球受力分析,利用力的合成与分解和共点力的平衡可求出E1、B1.
(2)由图可知,小球在x轴上方做匀速圆周运动,可判断受到的重力和电场力平衡,由二力平衡和可求出电场E2的大小和方向.
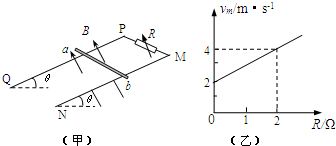
(3)小球在x轴上方做匀速圆周运动,由几何关系可求出轨道半径R为$\frac{5}{3}$,向心力提供洛伦兹力,结合牛顿第二定律即可求出磁场B2的大小,由左手定则可判断方向.
解答 解:(1)小球从M向N做匀速直线运动,可知小球所受合外力为零,对小球受力分析(如图一所示),
受到重力、电场力和洛伦兹力作用,由小球的受力可知小球带正电,
有: tanθ=$\frac{q{E}_{1}}{mg}$,θ=53°,
tanθ=$\frac{q{E}_{1}}{mg}$,θ=53°,
解得:E1=20V/m,
洛伦兹力的大小与电场力和重力的合力大小相等,有:qvB1=$\frac{mg}{cos53°}$,
解得:B1=5T;
(2)小球x轴上方做匀速圆周运动(如图二所示),可知电场力与重力平衡,
所以有: E2=$\frac{mg}{q}$,代入数据解得:E2=15N/C,因小球带正电,所以E2方向沿y轴正方向.
E2=$\frac{mg}{q}$,代入数据解得:E2=15N/C,因小球带正电,所以E2方向沿y轴正方向.
(3)设小球在x轴上方做匀速圆周运动的半径为R,
由几何关系(如图二)可得:Rsin53°+R=ON
则:ON=OMtan37°,
解得:R=$\frac{5}{3}$m,
小球做匀速圆周运动的向心力由洛伦兹力提供,由牛顿第二定律有:
qvB2=m$\frac{{v}^{2}}{R}$,
解得:B2=$\frac{mv}{qR}$,代入数据解得:B2=4.5T;
因小球带正电,由左手定则可知磁感应强度B2的方向垂直纸面向里.
答:(1)电场强度E1大小为20V/m,磁感应强度B1的大小为5T;
(2)电场E2的大小为15N/C,方向为沿y轴的正方向.
(3)磁场B2的大小为4.5T,方向为垂直纸面向里.
点评 该题考察了带电粒子在复合场中的运动.带电粒子在复合场中的运动情况有很多,常见的运动情况有如下几种:
1.带电粒子在复合场中所受的合外力为零时,粒子将处于静止状态或做匀速直线运动运动.
2.当带电粒子所受的合外力时刻指向一个圆心充当向心力时,粒子将做匀速圆周运动(如:电场力和重力相平衡,洛伦兹力提供向心力).
3.当带电粒子所受的合外力大小、方向均不断发生变化时,则粒子将非匀变速做曲线运动.
解决此类问题的关键是正确的对粒子进行受力分析和运动的分析,并结合草图进行解答.

 阅读快车系列答案
阅读快车系列答案 现代战争是科技之战、信息之战,某集团军进行的一次实战演习过程,在基地导演部的大型显示屏上一览无余,如图1所示是蓝军由基地A分三路大军进攻红军基地B的显示,若用x1、x2和x3分别表示三路大军的位移,则由大屏幕的显示图可知( )
现代战争是科技之战、信息之战,某集团军进行的一次实战演习过程,在基地导演部的大型显示屏上一览无余,如图1所示是蓝军由基地A分三路大军进攻红军基地B的显示,若用x1、x2和x3分别表示三路大军的位移,则由大屏幕的显示图可知( )| A. | x1>x2>x3 | B. | x1<x2<x3 | ||
| C. | x1=x2=x3 | D. | 三者关系无法确定 |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
| A. | 研究跳水运动员转体动作时,运动员可视为质点 | |
| B. | 静止的物体一定不受滑动摩擦力 | |
| C. | 速度大的物体惯性大,速度小的物体惯性小 | |
| D. | 静止于桌面上的书,受到桌面的支持力是因为桌面发生形变而产生 |
| A. | s=$\frac{a{t}^{2}}{2}$ | B. | T=$\frac{2π}{ω}$ | C. | I=$\frac{?}{R+r}$ | D. | E=$\frac{F}{q}$ |