题目内容
9．一物体作匀加速直线运动，通过一段位移8m所用的时间为4s，紧接着通过下一段8m位移所用时间为2s．则物体运动的加速度为（ ）m/s2．| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | 1 | D． | $\frac{4}{3}$ |
分析 根据匀变速直线运动中间时刻的瞬时速度等于这段位移的平均速度，可以求得两部分位移的中间时刻的瞬时速度，再由加速度的公式可以求得加速度的大小．
解答 解：物体作匀加速直线运动在前一段x所用的时间为t1，平均速度为：v1=$\frac{x}{{t}_{1}}$=$\frac{8}{4}$=2m/s，即为2s时刻的瞬时速度；
物体在后一段△x所用的时间为t2，平均速度为：v2=$\frac{x}{{t}_{2}}$=$\frac{8}{2}$=4m/s，即为5s末速度，
所以加速度为：a=$\frac{{v}_{2}-{v}_{1}}{t}$=$\frac{4-2}{5-2}$=$\frac{2}{3}$m/s2
故选：B
点评 利用匀变速直线运动中间时刻的瞬时速度等于这段位移的平均速度这个结论，可以很容易的做出这道题，本题就是考查学生对匀变速直线运动规律的理解．
练习册系列答案
相关题目
17．
如图所示，刚性板AB放在竖直墙壁和挡板K之间，竖直墙壁和水平面光滑，物体P、Q静止叠放在板上，此时物体P的上表面水平．若将K往右缓慢移动一小段距离后固定，整个装置在新的位置仍保持静止，与原来的相比（ ）
如图所示，刚性板AB放在竖直墙壁和挡板K之间，竖直墙壁和水平面光滑，物体P、Q静止叠放在板上，此时物体P的上表面水平．若将K往右缓慢移动一小段距离后固定，整个装置在新的位置仍保持静止，与原来的相比（ ）| A． | Q受到的摩擦力仍然为零 | B． | 板对P的支持力大小不变 | ||
| C． | 板对P的作用力大小不变 | D． | 板对P的摩擦力大小变大 |
1．
如图所示，在光滑绝缘的水平面上方，有两个方向相反的水平方向的匀强磁场，PQ为两磁场的边界，磁场范围足够大，磁感应强度的大小分别为B1=B，B2=2B，一个竖直放置的边长为a、质量为m、电阻为R的正方形金属线框，以初速度v垂直磁场方向从图中实线位置开始向右运动，当线框运动到在每个磁场中各有一半的面积时，线框的速度为$\frac{v}{2}$，则下列判断正确的是（ ）
如图所示，在光滑绝缘的水平面上方，有两个方向相反的水平方向的匀强磁场，PQ为两磁场的边界，磁场范围足够大，磁感应强度的大小分别为B1=B，B2=2B，一个竖直放置的边长为a、质量为m、电阻为R的正方形金属线框，以初速度v垂直磁场方向从图中实线位置开始向右运动，当线框运动到在每个磁场中各有一半的面积时，线框的速度为$\frac{v}{2}$，则下列判断正确的是（ ）| A． | 此过程中通过线框截面的电量为$\frac{3B{a}^{2}}{2R}$ | |
| B． | 此过程中线框克服安培力做的功为$\frac{3}{8}$mv2 | |
| C． | 此时线框的加速度为$\frac{9{B}^{2}{a}^{2}v}{2mR}$ | |
| D． | 此时线框中的电功率为$\frac{9{B}^{2}{a}^{2}{v}^{2}}{2R}$ |
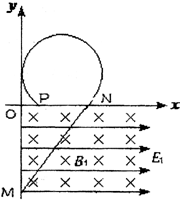如图所示，在x轴下方存在着正交的电场与磁场，电场方向沿x轴正方向，电场强度大小为E1，磁场方向垂直纸面向里，磁感应强度大小为B1．一个质量m=3g，电荷量q=2×10-3 C的带正电小球自y轴上的M点沿直线匀速运动到x轴上的N点，速度大小v=5 m/s，方向与水平方向成θ=53°角，且已知OM=4 m．在x轴上方存在正交的匀强电场E2与匀强磁场B2（图中均未画出），小球在x轴上方做圆周运动，恰好与y轴相切，运动轨迹如图所示．（g=10 m/s2，sin53°=0.8）求：
如图所示，一个电阻不计的导体棒ab放在电阻不计的足够长的导轨上（导轨间距为L），他们接触良好，导轨光滑，导轨与水平面间的夹角为θ；导轨上边接一个阻值为R的电阻，一磁感强度为B的匀强磁场垂直导轨表面向上，ab棒质量为m，重力加速度为g；现将ab棒由静止释放，求：