题目内容
4. 如图所示,相距s=6m、质量均为m的木板A、B(A、B两木板完全相同)置于水平地面上,一质量为2m、可视为质点的物块C置于木板A的左端.已知物块C与木板A、B之间的动摩擦因数均为μ1=0.22,木板A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可以认为等于滑动摩擦力,开始时,三个物体均处于静止状态.现给物块C施加一个水平方向右的恒力F,且F=0.4mg,已知木板A、B碰撞后立即粘连在一起,且碰后瞬间两者的速度为木板A碰前速度的一半.碰后瞬间C的速度不变.g=10m/s2,求:
如图所示,相距s=6m、质量均为m的木板A、B(A、B两木板完全相同)置于水平地面上,一质量为2m、可视为质点的物块C置于木板A的左端.已知物块C与木板A、B之间的动摩擦因数均为μ1=0.22,木板A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可以认为等于滑动摩擦力,开始时,三个物体均处于静止状态.现给物块C施加一个水平方向右的恒力F,且F=0.4mg,已知木板A、B碰撞后立即粘连在一起,且碰后瞬间两者的速度为木板A碰前速度的一半.碰后瞬间C的速度不变.g=10m/s2,求:(1)物块C开始运动时的加速度;
(2)从物块C开始运动到木板A与B相碰所经历的时间.
(3)已知木板A、B的长度均为L=0.6m,请通过分析计算后判断:物块C最终会不会从木板上掉下来?
分析 (1)设木板A与物块C之间的滑动摩擦力大小为f1,木板A与水平地面之间的滑动摩擦力大小为f2,根据f1和f2的关系判断知道A与B碰前A与C是一起向右做匀加速直线运动,设此过程中它们的加速度为a,根据牛顿第二定律求a.
(2)根据运动学位移公式列式,可求得从物块C开始运动到木板A与B相碰所经历的时间,以及A与木板B相碰时的速度υ.
(3)碰撞后瞬间,物块C的速度不变,根据牛顿第二定律求出物块C在木板上滑动的加速度,当三者的速度相同时,不掉下就不会掉下,根据运动学基本公式即可求解.
解答 解:(1)设木板A与物块C之间的滑动摩擦力大小为f1,木板A与水平地面之间的滑动摩擦力大小为f2,
有:f1=2μ1mg=0.44mg,f2=μ2(2mg+mg)=0.3Mg
可见f2<F<f1,故可知在木板A、B相碰前,在F的作用下,木板A与物块C一起水平向右做匀加速直线运动.
设此过程中它们的加速度为a,由牛顿第二定律得
F-f2=(2m+m)a
解得 a=$\frac{0.1g}{3}$=$\frac{1}{3}m/{s}^{2}$
(2)设从物块C开始运动到木板A与B相碰所经历的时间为t,A与木板B相碰时的速度为υ,
有:s=$\frac{1}{2}a{t}^{2}$,υ=at
解得:t=6s,υ=2m/s.
(3)碰撞后瞬间,物块C的速度不变,设A、B碰后速度为υ',即有 v′=$\frac{v}{2}$
此即木板A、B共同运动的初速度.
此后,物块C在木板上滑动时的加速度为:ac=$\frac{F-{f}_{1}}{2m}$=-0.2m/s2.
物块C在木板上滑动时,木板A、B共同运动的加速度为:aAB=$\frac{{f}_{1}-{f}_{2}^{′}}{2m}$
其中 f2′=μ2(2mg+2mg)=0.4mg
解得:aAB=0.2m/s2.
若木板A、B很长,则物块C不会掉下来.设物块C再运动时间t1后,三者的速度相同,有:υ+act1=$\frac{v}{2}$+aABt1,
代入数据解得:t1=2.5s
在此过程中,物块C的位移为:sc=υt1+$\frac{1}{2}$act12.
解得 sc=4.375m
木板A、B的位移为:sAB=$\frac{v}{2}$t1+$\frac{1}{2}$aABt12=3.125m
由于sc-sAB=1.25m>LA+LB=1.2m,可见物块C最终会从木板上掉下来.
答:
(1)物块C开始运动时的加速度为$\frac{1}{3}m/{s}^{2}$.
(2)从物块C开始运动到木板A与B相碰所经历的时间t为6s.
(3)物块C最终会从木板上掉下来.
点评 本题的关键是通过受力分析,明确各个物体的运动情况,分段运用牛顿第二定律及运动学基本公式综合列式求解.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案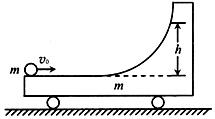 如图所示,质量为m的小车静置于光滑水平面上,小车右端带有光滑圆弧轨道,一质量也为m的小球以水平速度v0从左端冲上小车,到达某一高度h后又能回到小车左端,重力加速度为g,不计一切摩擦,以下说法正确的是( )
如图所示,质量为m的小车静置于光滑水平面上,小车右端带有光滑圆弧轨道,一质量也为m的小球以水平速度v0从左端冲上小车,到达某一高度h后又能回到小车左端,重力加速度为g,不计一切摩擦,以下说法正确的是( )| A. | 小球回到小车左端时速度为v0 | B. | 小球回到小车左端时速度为0 | ||
| C. | $h=\frac{v_0^2}{2g}$ | D. | $h=\frac{v_0^2}{4g}$ |
| A. | 由波尔理论的原子模型可以推知,氢原子处于激发态,量子数越大,核外电子动能越小 | |
| B. | 汤姆逊通过对阴极射线的研究发现了电子,并提出了原子核式结构学说 | |
| C. | 德布罗意指出微观粒子的动量越大,其对应的波长就越长 | |
| D. | 现已建成的核电站的能量均来自于核聚变 |
 如图所示,质量为m的小球从P点开始做自由落体运动,由位置A进入水中之后,受到水对它竖直向上的作用力,其大小与小球的速度成正比.小球运动到B点后开始做匀速直线运动.已知PA、AB、BC段的高度均为h,设小球在PA段的运动时间为t1,在AB段运动的时间为t2,在BC段运动时间为t3.空气阻力不计,则下列说法中一定错误的是( )
如图所示,质量为m的小球从P点开始做自由落体运动,由位置A进入水中之后,受到水对它竖直向上的作用力,其大小与小球的速度成正比.小球运动到B点后开始做匀速直线运动.已知PA、AB、BC段的高度均为h,设小球在PA段的运动时间为t1,在AB段运动的时间为t2,在BC段运动时间为t3.空气阻力不计,则下列说法中一定错误的是( )| A. | t1>t2>t3 | |
| B. | 在AB段和BC段水对小球的作用力所做的功相等 | |
| C. | 小球在AB段运动时的机械能增大,在BC段运动时机械能减小 | |
| D. | 从A点到B点,合力对小球做正功 |
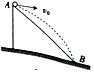 如图所示,小球从斜面的顶端A处以大小为v0的初速度水平抛出,恰好落到斜面底部的B点,且此时的速度大小vB=$\sqrt{5}$v0,空气阻力不计,该斜面的倾角为( )
如图所示,小球从斜面的顶端A处以大小为v0的初速度水平抛出,恰好落到斜面底部的B点,且此时的速度大小vB=$\sqrt{5}$v0,空气阻力不计,该斜面的倾角为( )| A. | 30° | B. | 37° | C. | 45° | D. | 60° |
 “套圈游戏”深受大家的喜爱,游戏者要站到区域线将圈圈水平抛出,落地时套中的物体即为“胜利品”.某次一小孩和大人分别站在同一位置都想套住同一物体,下列做法可行的是( )
“套圈游戏”深受大家的喜爱,游戏者要站到区域线将圈圈水平抛出,落地时套中的物体即为“胜利品”.某次一小孩和大人分别站在同一位置都想套住同一物体,下列做法可行的是( )| A. | 大人和小孩以相同速度抛出 | |
| B. | 大人以较小速度抛出 | |
| C. | 大人蹲下与孩子等高并后退,以较大速度抛出 | |
| D. | 大人后退站立,以相同速度抛出 |

 2016年9月15日,“天宫二号”空间实验室在酒泉卫星发射中心发射成功.“天宫二号”是中国第一个真正意义上的空间实验室.在“天宫二号”除了要验证航天员在轨中期驻留,还将开展14项空间科学和应用实验.10月19日“神州十一号”飞船与在距地面高度为h的圆轨道上运行的“天宫二号”教会对接成功,航天员景海鹏、陈冬进入“天宫二号”.航天员此次在“天宫二号”中期驻留时间为t.
2016年9月15日,“天宫二号”空间实验室在酒泉卫星发射中心发射成功.“天宫二号”是中国第一个真正意义上的空间实验室.在“天宫二号”除了要验证航天员在轨中期驻留,还将开展14项空间科学和应用实验.10月19日“神州十一号”飞船与在距地面高度为h的圆轨道上运行的“天宫二号”教会对接成功,航天员景海鹏、陈冬进入“天宫二号”.航天员此次在“天宫二号”中期驻留时间为t. 如图所示,将质量m=1.0kg的小物块放在长L=3.0m的平板车左端,车的上表面粗糙,物块与车上表面间的动摩擦因数μ=0.6,光滑半圆形固定轨道与光滑水平轨道在同一竖直平面内,半圆形轨道的半径r=1.2m,直径MON竖直,车的上表面和轨道最低点高度相同,开始时车和物块一起以v0=10m/s的初速度在水平轨道上向右运动,车碰到轨道后立即停止运动,取g=10m/s2,求:
如图所示,将质量m=1.0kg的小物块放在长L=3.0m的平板车左端,车的上表面粗糙,物块与车上表面间的动摩擦因数μ=0.6,光滑半圆形固定轨道与光滑水平轨道在同一竖直平面内,半圆形轨道的半径r=1.2m,直径MON竖直,车的上表面和轨道最低点高度相同,开始时车和物块一起以v0=10m/s的初速度在水平轨道上向右运动,车碰到轨道后立即停止运动,取g=10m/s2,求: