题目内容
9.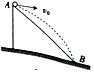 如图所示,小球从斜面的顶端A处以大小为v0的初速度水平抛出,恰好落到斜面底部的B点,且此时的速度大小vB=$\sqrt{5}$v0,空气阻力不计,该斜面的倾角为( )
如图所示,小球从斜面的顶端A处以大小为v0的初速度水平抛出,恰好落到斜面底部的B点,且此时的速度大小vB=$\sqrt{5}$v0,空气阻力不计,该斜面的倾角为( )| A. | 30° | B. | 37° | C. | 45° | D. | 60° |
分析 根据平行四边形定则求出小球落地时的竖直分速度,结合速度时间公式求出运动的时间,抓住竖直位移和水平位移的关系求出斜面的倾角.
解答 解:根据平行四边形定则知,落到底端时竖直分速度为:
${v}_{y}=\sqrt{{{v}_{B}}^{2}-{{v}_{0}}^{2}}=2{v}_{0}$,
则运动的时间为:t=$\frac{{v}_{y}}{g}=\frac{2{v}_{0}}{g}$,
设斜面的倾角为θ,则有:tanθ=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}=1$,解得θ=45°,故C正确,ABD错误.
故选:C.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,也可以结合平抛运动速度与水平方向夹角正切值是位移与水平方向夹角正切值的2倍进行求解.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
4. 真空中有一个正方体区域abfe-dcgh,有一对等量异种点电荷分别位于正方体的顶点a和f处,现在各顶点间移动一正试探电荷,关于该试探电荷所受的电场力和具有的电势能,以下判断正确的是( )
真空中有一个正方体区域abfe-dcgh,有一对等量异种点电荷分别位于正方体的顶点a和f处,现在各顶点间移动一正试探电荷,关于该试探电荷所受的电场力和具有的电势能,以下判断正确的是( )
 真空中有一个正方体区域abfe-dcgh,有一对等量异种点电荷分别位于正方体的顶点a和f处,现在各顶点间移动一正试探电荷,关于该试探电荷所受的电场力和具有的电势能,以下判断正确的是( )
真空中有一个正方体区域abfe-dcgh,有一对等量异种点电荷分别位于正方体的顶点a和f处,现在各顶点间移动一正试探电荷,关于该试探电荷所受的电场力和具有的电势能,以下判断正确的是( )| A. | 在d点和g点所受电场力大小相等、方向相同 | |
| B. | 在h点和c点所受电场力大小相等、方向相同 | |
| C. | 在d点和g点电势能相等 | |
| D. | 在h点和c点电势能相等 |
1.下列运动过程中机械能守恒的是( )
| A. | 跳伞运动员打开降落伞在竖直方向向下做匀速直线运动 | |
| B. | 小球在竖直光滑圆轨道内做圆周运动 | |
| C. | 摩天轮在竖直平面内匀速转动时,舱内的乘客做匀速圆周运动 | |
| D. | 带电小球仅在电场力作用下做加速运动 |
18.某电场中a、b两点间的电势差为200V,将一点电荷从a点移到b点电场力做功1.0×10-3J.该电荷的电荷量为( )
| A. | 2.0×105C | B. | 5.0×10-6C | C. | 0.2C | D. | 0.5C |
19.用α粒子轰击铝核(2713A1),在生成磷核(3015P)的同时释放一个x粒子,磷核(3015P)具有放射性,它在衰变为硅核(3014Si)的同时释放一个y粒子,则x粒子和y粒子分別是( )
| A. | .中子和正电子 | B. | 质子和正电子 | C. | 中子和电子 | D. | 质子和电子 |
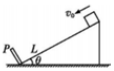 足够长的倾角为θ的粗糙斜面上,有一质量为m的滑块距挡板P为L,以初速度v0沿斜面下滑,并与挡板发生碰撞,滑块与斜面动摩擦因数为μ,μ<tanθ.若滑块与挡板碰撞没有机械能损失,求:
足够长的倾角为θ的粗糙斜面上,有一质量为m的滑块距挡板P为L,以初速度v0沿斜面下滑,并与挡板发生碰撞,滑块与斜面动摩擦因数为μ,μ<tanθ.若滑块与挡板碰撞没有机械能损失,求: 如图所示,相距s=6m、质量均为m的木板A、B(A、B两木板完全相同)置于水平地面上,一质量为2m、可视为质点的物块C置于木板A的左端.已知物块C与木板A、B之间的动摩擦因数均为μ1=0.22,木板A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可以认为等于滑动摩擦力,开始时,三个物体均处于静止状态.现给物块C施加一个水平方向右的恒力F,且F=0.4mg,已知木板A、B碰撞后立即粘连在一起,且碰后瞬间两者的速度为木板A碰前速度的一半.碰后瞬间C的速度不变.g=10m/s2,求:
如图所示,相距s=6m、质量均为m的木板A、B(A、B两木板完全相同)置于水平地面上,一质量为2m、可视为质点的物块C置于木板A的左端.已知物块C与木板A、B之间的动摩擦因数均为μ1=0.22,木板A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可以认为等于滑动摩擦力,开始时,三个物体均处于静止状态.现给物块C施加一个水平方向右的恒力F,且F=0.4mg,已知木板A、B碰撞后立即粘连在一起,且碰后瞬间两者的速度为木板A碰前速度的一半.碰后瞬间C的速度不变.g=10m/s2,求: 如图所示,在竖直平面内有一半径R=10m的圆弧轨道ADB与一倾角θ=60°斜面轨道AC在A点处平滑连接,半径OB 竖直.一质量m=1.0kg的滑块自斜面上高度H=4.5R的C点由静止开始下滑,到达圆轨道最高点B 时恰好对轨道没有压力,滑块与斜面间摩擦因数为μ,圆弧轨道光滑.求
如图所示,在竖直平面内有一半径R=10m的圆弧轨道ADB与一倾角θ=60°斜面轨道AC在A点处平滑连接,半径OB 竖直.一质量m=1.0kg的滑块自斜面上高度H=4.5R的C点由静止开始下滑,到达圆轨道最高点B 时恰好对轨道没有压力,滑块与斜面间摩擦因数为μ,圆弧轨道光滑.求