题目内容
7.一只电子钟的时针和分针的长度之比为2:3,它们的周期之比为12:1,时针和分针端的角速度之比为1:12,线速度之比为1:18.分析 时针和分针都是做匀速圆周运动,周期分别为12h、1h;根据角速度与周期关系ω=$\frac{2π}{T}$求解角速度之比;根据线速度与角速度关系v=Rω求解线速度之比.
解答 解:电子钟的时针和分针都是做匀速圆周运动,周期分别为12h、1h,故周期比为12:1;
根据ω=$\frac{2π}{T}$,可得时针和分针端的角速度之比为1:12;
根据v=Rω,线速度之比为:
v1:v2=ω1r1:ω2r2=1×2:12×3=1:18;
故答案为:12:1; 1:12; 1:18
点评 考查圆周运动线速度,角速度,周期的关系,解题关键是记住角速度与周期关系ω=$\frac{2π}{T}$,线速度与角速度关系v=Rω.

练习册系列答案
相关题目
6. 如图所示,A、B 两小球由绕过轻质定滑轮的细线相连,A 放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为 k 的轻质弹簧相连,C 球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A 的质量为 4m,B、C 的质量均为 m,重力加速度为 g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放 A 后,A 沿斜面下滑至速度最大时 C 恰好离开地面.下列说法正确的是( )
如图所示,A、B 两小球由绕过轻质定滑轮的细线相连,A 放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为 k 的轻质弹簧相连,C 球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A 的质量为 4m,B、C 的质量均为 m,重力加速度为 g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放 A 后,A 沿斜面下滑至速度最大时 C 恰好离开地面.下列说法正确的是( )
 如图所示,A、B 两小球由绕过轻质定滑轮的细线相连,A 放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为 k 的轻质弹簧相连,C 球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A 的质量为 4m,B、C 的质量均为 m,重力加速度为 g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放 A 后,A 沿斜面下滑至速度最大时 C 恰好离开地面.下列说法正确的是( )
如图所示,A、B 两小球由绕过轻质定滑轮的细线相连,A 放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为 k 的轻质弹簧相连,C 球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A 的质量为 4m,B、C 的质量均为 m,重力加速度为 g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放 A 后,A 沿斜面下滑至速度最大时 C 恰好离开地面.下列说法正确的是( )| A. | 斜面倾角α=30° | B. | A球获得最大速度为2g$\sqrt{\frac{m}{5k}}$ | ||
| C. | C刚离开地面时,B球的加速度最大 | D. | 斜面倾角α=45° |
7.下列说法正确的是( )
| A. | X射线是处于激发态的原子核辐射出来的 | |
| B. | 康普顿效应和电子的衍射现象说明光和电子都具有波动性 | |
| C. | 普朗克为了解释黑体辐射现象,第一次提出了能量量子化理论 | |
| D. | 汤姆孙根据阴极射线在电场和磁场中的偏转情况断定其本质是带负电的粒子流并测定了这种粒子的电荷量 |
15. 2015年6月9日,杭州一家游乐园附近发生电力故障,导致正在运行的过山车停住,12名乘客都在轨道顶端,脑袋朝下挂在空中,当地消防部门架起云梯,花费了半个小时,才解救出被困的游客.但坐过过山车的人知道,在运行到轨道最高点时并没有倒挂的感觉,并且觉得牢牢的坐在座位上.若过山车的轨道半径R=20m,g=10m/s2.人在最高点若没有倒挂感觉,过山车速度不得小于( )
2015年6月9日,杭州一家游乐园附近发生电力故障,导致正在运行的过山车停住,12名乘客都在轨道顶端,脑袋朝下挂在空中,当地消防部门架起云梯,花费了半个小时,才解救出被困的游客.但坐过过山车的人知道,在运行到轨道最高点时并没有倒挂的感觉,并且觉得牢牢的坐在座位上.若过山车的轨道半径R=20m,g=10m/s2.人在最高点若没有倒挂感觉,过山车速度不得小于( )
 2015年6月9日,杭州一家游乐园附近发生电力故障,导致正在运行的过山车停住,12名乘客都在轨道顶端,脑袋朝下挂在空中,当地消防部门架起云梯,花费了半个小时,才解救出被困的游客.但坐过过山车的人知道,在运行到轨道最高点时并没有倒挂的感觉,并且觉得牢牢的坐在座位上.若过山车的轨道半径R=20m,g=10m/s2.人在最高点若没有倒挂感觉,过山车速度不得小于( )
2015年6月9日,杭州一家游乐园附近发生电力故障,导致正在运行的过山车停住,12名乘客都在轨道顶端,脑袋朝下挂在空中,当地消防部门架起云梯,花费了半个小时,才解救出被困的游客.但坐过过山车的人知道,在运行到轨道最高点时并没有倒挂的感觉,并且觉得牢牢的坐在座位上.若过山车的轨道半径R=20m,g=10m/s2.人在最高点若没有倒挂感觉,过山车速度不得小于( )| A. | 15.1m/s | B. | 20.0m/s | C. | 16.7m/s | D. | 17.3m/s |
16.同步卫星离地心距离为r,运行速率为v1,向心加速度为a1,轨道所在处的重力加速度为g1.地球的半径为R,第一宇宙速度为v2,地球赤道上的物体随地球自转的向心加速度为a2,地球表面的重力加速度为g2.则下列结果不正确的是( )
| A. | a1=g1 | B. | $\frac{{g}_{1}}{{g}_{2}}$=$\frac{{R}^{2}}{{r}^{2}}$ | C. | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{r}{R}$ | D. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{r}{R}$ |
17. 如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦),当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中( )
如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦),当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中( )
 如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦),当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中( )
如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦),当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中( )| A. | 物体A也做匀速直线运动 | |
| B. | 绳子拉力始终大于物体A所受的重力 | |
| C. | 绳子对A的拉力逐渐减小 | |
| D. | 地面对物体B的支持力逐渐增大 |
 如图所示,质量为m的正方体小滑块从高为h、倾角α=53°的斜面顶端A点由静止释放,运动到斜面底端B点后进入一半径为R的$\frac{1}{2}$光滑细圆管内(B点处有一段长度可忽略的圆弧,圆管内径略大于小滑块的边长),已知小滑块在运动过程中始终受到一水平向左的外力F=$\frac{3}{4}$mg作用,g为重力加速度,小滑块恰好能到达D点,OD与竖直直径BC的夹角β=37°,sin53°=0.8,cos53°=0.6.求:
如图所示,质量为m的正方体小滑块从高为h、倾角α=53°的斜面顶端A点由静止释放,运动到斜面底端B点后进入一半径为R的$\frac{1}{2}$光滑细圆管内(B点处有一段长度可忽略的圆弧,圆管内径略大于小滑块的边长),已知小滑块在运动过程中始终受到一水平向左的外力F=$\frac{3}{4}$mg作用,g为重力加速度,小滑块恰好能到达D点,OD与竖直直径BC的夹角β=37°,sin53°=0.8,cos53°=0.6.求: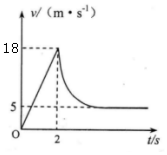 低空跳伞是一种危险性很高的极限运动,通常从高楼、悬崖、高塔等固定物上起跳,在极短时间内必须打开降落伞,才能保证着地安全,某跳伞运动员从高H=100m的楼层起跳,自由下落一段时间后打开降落伞,最终以安全速度匀速落地.若降落伞视为瞬间打开,得到运动员起跳后的速度v随时间t变化的图象如图所示,已知运动员及降落伞装备的总质量m=60kg,开伞后所受阻力大小与速率成正比,即f=kv,取g=10m/s2,求:
低空跳伞是一种危险性很高的极限运动,通常从高楼、悬崖、高塔等固定物上起跳,在极短时间内必须打开降落伞,才能保证着地安全,某跳伞运动员从高H=100m的楼层起跳,自由下落一段时间后打开降落伞,最终以安全速度匀速落地.若降落伞视为瞬间打开,得到运动员起跳后的速度v随时间t变化的图象如图所示,已知运动员及降落伞装备的总质量m=60kg,开伞后所受阻力大小与速率成正比,即f=kv,取g=10m/s2,求:



