题目内容
15．
2015年6月9日，杭州一家游乐园附近发生电力故障，导致正在运行的过山车停住，12名乘客都在轨道顶端，脑袋朝下挂在空中，当地消防部门架起云梯，花费了半个小时，才解救出被困的游客．但坐过过山车的人知道，在运行到轨道最高点时并没有倒挂的感觉，并且觉得牢牢的坐在座位上．若过山车的轨道半径R=20m，g=10m/s2．人在最高点若没有倒挂感觉，过山车速度不得小于（ ）| A． | 15.1m/s | B． | 20.0m/s | C． | 16.7m/s | D． | 17.3m/s |
分析 人在最高点若没有倒挂感觉，并且觉得牢牢的坐在座位上，临界情况是人对座椅的压力为mg，靠重力和弹力的合力提供向心力，结合牛顿第二定律求出最高点的最小速度．
解答 解：人在最高点若没有倒挂感觉，并且觉得牢牢的坐在座位上，临界情况是人对座椅的压力为mg，根据牛顿第二定律，有：F+mg=m$\frac{{v}^{2}}{R}$，
F=mg，
解得过山车的最小速度$v=\sqrt{2gR}=\sqrt{2×10×20}$m/s=20m/s．故B正确，A、C、D错误．
故选：B．
点评 解决本题的关键知道最高点的向心力来源，抓住临界状态，结合牛顿第二定律进行求解，难度不大．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
14．关于机械波的形成，下列说法中正确的是（ ）
| A． | 物体做机械振动，一定产生机械波 | |
| B． | 后振动的质点总是跟着先振动的质点振动，只是时间上落后一步 | |
| C． | 参与振动的质点有相同的频率 | |
| D． | 机械波在传播过程中，各质点并不随波迁移，传递的是振动形式和能量 |
15．
如图所示，竖直薄壁圆筒内壁光滑、半径为R，上部侧面A处开有小口，在小口A的正下方h处亦开有与A大小相同的小口B，小球从小口A沿切线方向水平射入筒内，使小球紧贴筒内壁运动，要使小球从B口处飞出，小球进入A口的速度v0可能为（ ）
如图所示，竖直薄壁圆筒内壁光滑、半径为R，上部侧面A处开有小口，在小口A的正下方h处亦开有与A大小相同的小口B，小球从小口A沿切线方向水平射入筒内，使小球紧贴筒内壁运动，要使小球从B口处飞出，小球进入A口的速度v0可能为（ ）| A． | πR$\sqrt{\frac{g}{2h}}$ | B． | πR$\sqrt{\frac{2g}{h}}$ | C． | 4πR$\sqrt{\frac{g}{2h}}$ | D． | 4πR$\sqrt{\frac{2g}{h}}$ |
3．
如图所示，倒悬的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A，活塞A的下面吊着一个重物，汽缸中封闭着一定质量的理想气体．起初各部分均静止不动，大气压强保持不变．对于汽缸内的气体，当其状态缓慢发生变化时，下列判断正确的是（ ）
如图所示，倒悬的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A，活塞A的下面吊着一个重物，汽缸中封闭着一定质量的理想气体．起初各部分均静止不动，大气压强保持不变．对于汽缸内的气体，当其状态缓慢发生变化时，下列判断正确的是（ ）| A． | 若环境温度升高，则气体的压强一定增大 | |
| B． | 保持环境温度不变，缓慢增加重物的质量，气体一定会吸热 | |
| C． | 当活塞向下移动时，外界一定对气体做正功 | |
| D． | 若环境温度降低，缓慢增加重物的质量，气体体积可能保持不变 |
10．
如图所示，在光滑水平面上方，有两个磁感应强度大小均为B、方向相反的水平匀强磁场，PQ为两个磁场的边界，磁场范围足够大．一个边长为L，质量为m，电阻为R的正方形金属线框沿垂直磁场方向，以速度v从图示位置向右运动，运动过程中线框始终与磁场垂直当线框中心线AB运动到与PQ重合时，线框的速度为$\frac{v}{2}$，则（ ）
如图所示，在光滑水平面上方，有两个磁感应强度大小均为B、方向相反的水平匀强磁场，PQ为两个磁场的边界，磁场范围足够大．一个边长为L，质量为m，电阻为R的正方形金属线框沿垂直磁场方向，以速度v从图示位置向右运动，运动过程中线框始终与磁场垂直当线框中心线AB运动到与PQ重合时，线框的速度为$\frac{v}{2}$，则（ ）| A． | 此时线框的电功率为$\frac{4{B}^{2}{L}^{2}{v}^{2}}{R}$ | |
| B． | 此时线框的加速度为$\frac{4{B}^{2}{L}^{2}v}{mR}$ | |
| C． | 此过程通过线框截面的电荷量为$\frac{B{L}^{2}}{R}$ | |
| D． | 此过程回路产生的电能为0.375mv2 |
20．
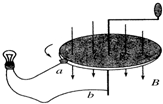如图所示是法拉第做成的世界上第一台发电机模型的原理图．将铜盘放在磁场中，让磁感线垂直穿过铜盘；图中a、b导线与铜盘的中轴线处在同一平面内；转动铜盘，就可以使闭合电路获得电流．若图中铜盘半径为L，匀强磁场的磁感应强度为B，回路总电阻为R，从上往下看逆时针匀速转动铜盘的角速度为ω．则下列说法正确的是（ ）
如图所示是法拉第做成的世界上第一台发电机模型的原理图．将铜盘放在磁场中，让磁感线垂直穿过铜盘；图中a、b导线与铜盘的中轴线处在同一平面内；转动铜盘，就可以使闭合电路获得电流．若图中铜盘半径为L，匀强磁场的磁感应强度为B，回路总电阻为R，从上往下看逆时针匀速转动铜盘的角速度为ω．则下列说法正确的是（ ）| A． | 回路中有大小和方向作周期性变化的电流 | |
| B． | 回路中电流大小恒定，且等于$\frac{{B{L^2}ω}}{2R}$ | |
| C． | 回路中电流方向不变，且从b导线流进灯泡，再从a导线流向旋转的铜盘 | |
| D． | 回路中电流方向不变．且从α导线流进灯泡．再从b导线流向旋转的铜盘 |
4．在离地面高度为h处竖直向上抛出一质量为m的物体，抛出时的速度为v0，当它落到地面时的速度为v，用g表示重力加速度，则在此过程中空气阻力对物体做的功为（ ）
| A． | $mgh-\frac{1}{2}m{v^2}-\frac{1}{2}mv_0^2$ | B． | $\frac{1}{2}m{v^2}-\frac{1}{2}mv_0^2+mgh$ | ||
| C． | $mgh+\frac{1}{2}mv_0^2-\frac{1}{2}m{v^2}$ | D． | $\frac{1}{2}m{v^2}-\frac{1}{2}mv_0^2-mgh$ |
如图所示，一条轨道固定在竖直平面内，粗糙的ab段水平足够长，bcde段光滑，cde段是以O为圆心，半径为R=0.4m的一小段圆弧，且O在ab的连线上，可视为质点的物块A和B紧靠在一起，静止于b处，mA=0.6kg．mB=0.1kg．两物块在足够大的内力作用下突然分离，分别向左、右始终沿轨道运动．B到d点时速度沿水平方向，此时轨道对B的支持力大小等于B所受重力的$\frac{3}{4}$．A与ab段的动摩擦因数为μ=0.1，重力加速度为g=10m/s2，求：