题目内容
18.某行星是质量分布均匀的球体,其密度为ρ,万有引力常量为G.当此行星自转角速度达到下列哪个值时,其赤道上的物体将要飞离行星表面( )| A. | $\sqrt{\frac{3π}{ρG}}$ | B. | $\sqrt{\frac{ρG}{3π}}$ | C. | $\frac{1}{2}\sqrt{3πρG}$ | D. | $2\sqrt{\frac{πρG}{3}}$ |
分析 本题中,赤道上物体飞离行星表面说明此时万有引力提供向心力,根据$\frac{GMm}{{R}^{2}}$=m$\frac{{4π}^{2}R}{{T}^{2}}$和公式M=ρV=$\frac{4ρ{πR}^{3}}{3}$可解题.
解答 解:设某行星质量为M,半径为R,物体质量为m,万有引力充当向心力,则有;
$\frac{GMm}{{R}^{2}}$=m$\frac{{4π}^{2}R}{{T}^{2}}$
M=ρV=$\frac{4ρ{πR}^{3}}{3}$
联立以上两式解得:T=$\sqrt{\frac{3π}{ρG}}$.
故选:A
点评 该题考查了万有引力公式及向心力基本公式的直接应用,难度不大,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
8. 如图所示,起重机用四根长度均为l的轻绳把货物从四角吊起,货物重为G,上表面是边长为l的正方形,当货物保持水平且匀速上升时,每根绳上的拉力大小为( )
如图所示,起重机用四根长度均为l的轻绳把货物从四角吊起,货物重为G,上表面是边长为l的正方形,当货物保持水平且匀速上升时,每根绳上的拉力大小为( )
 如图所示,起重机用四根长度均为l的轻绳把货物从四角吊起,货物重为G,上表面是边长为l的正方形,当货物保持水平且匀速上升时,每根绳上的拉力大小为( )
如图所示,起重机用四根长度均为l的轻绳把货物从四角吊起,货物重为G,上表面是边长为l的正方形,当货物保持水平且匀速上升时,每根绳上的拉力大小为( )| A. | $\frac{\sqrt{2}}{4}$G | B. | $\frac{\sqrt{3}}{6}$G | C. | $\frac{G}{2}$ | D. | $\frac{\sqrt{2}}{2}$G |
9. 如图,在木板上有一物体.在木板与水平面间的夹角缓慢增大的过程中,如果物体仍保持与板相对静止.则下列说法中错误的是( )
如图,在木板上有一物体.在木板与水平面间的夹角缓慢增大的过程中,如果物体仍保持与板相对静止.则下列说法中错误的是( )
 如图,在木板上有一物体.在木板与水平面间的夹角缓慢增大的过程中,如果物体仍保持与板相对静止.则下列说法中错误的是( )
如图,在木板上有一物体.在木板与水平面间的夹角缓慢增大的过程中,如果物体仍保持与板相对静止.则下列说法中错误的是( )| A. | 斜面对物体的弹力大小增加 | |
| B. | 斜面对物体的摩擦力大小增加 | |
| C. | 物体所受的弹力和重力的合力方向沿斜面向下 | |
| D. | 物体所受的合外力不变 |
6.一个质量为m的物体以a=2g的加速度竖直向下运动,则在此物体下降h高度的过程中,物体的( )
| A. | 重力势能减少了2mgh | B. | 机械能增加了mgh | ||
| C. | 动能增加了mgh | D. | 机械能保持不变 |
8.正弦交流电经过匝数比为$\frac{{n}_{1}}{{n}_{2}}$=$\frac{10}{1}$的变压器与电阻R交流电压表V、交流电流表A按如图甲所示方式连接,R=10Ω,图乙是R两端电压U随时间变化的图象,Um=10$\sqrt{2}$v,则下列说法中正确的是( )

| A. | 通过R的电流iR随时间t变化的规律是iR=$\sqrt{2}$sin100πt(A) | |
| B. | 电流表A的读数为0.1A | |
| C. | 电流表A的读数为$\frac{\sqrt{2}}{10}$A | |
| D. | 电压表的读数为Um=10$\sqrt{2}$v |
 某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并恰好越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=2.0W工作,进入竖直轨道前受到阻力f恒为0.3N,随后在运动中受到的阻力均可不计.图中L=4.00m,R=0.50m,h=1.25m,S=3.00m(取g=10m/s2)问:
某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并恰好越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=2.0W工作,进入竖直轨道前受到阻力f恒为0.3N,随后在运动中受到的阻力均可不计.图中L=4.00m,R=0.50m,h=1.25m,S=3.00m(取g=10m/s2)问: 如图1所示,一架直升飞机正在大海中的钻井平台上执行救援任务,救生员抱着受援者通过缆绳将其提升到飞机上.提升过程中飞机沿水平方向以10m/s的速度匀速飞离钻井平台.已知飞机离钻井平台的竖直高度为30m;救生员质量60kg;受援者40kg;提升过程中飞机上的力传感器测得缆绳对救生员的拉力如图2所示,g取10m/s2.求:
如图1所示,一架直升飞机正在大海中的钻井平台上执行救援任务,救生员抱着受援者通过缆绳将其提升到飞机上.提升过程中飞机沿水平方向以10m/s的速度匀速飞离钻井平台.已知飞机离钻井平台的竖直高度为30m;救生员质量60kg;受援者40kg;提升过程中飞机上的力传感器测得缆绳对救生员的拉力如图2所示,g取10m/s2.求: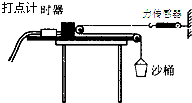 如图所示是测量物块与木板间动摩擦因数的实验装置.长木板固定在水平桌面上,打点计时器固定在长木板上,纸带穿过打点计时器,与带滑轮的物块相连.沙桶和力传感器通过绕在滑轮上的细绳相连.调整沙桶的质量,当放开沙桶时,使物块在木板上做匀加速直线运动.(重力加速度为g,滑轮的质量和摩擦可以忽略)
如图所示是测量物块与木板间动摩擦因数的实验装置.长木板固定在水平桌面上,打点计时器固定在长木板上,纸带穿过打点计时器,与带滑轮的物块相连.沙桶和力传感器通过绕在滑轮上的细绳相连.调整沙桶的质量,当放开沙桶时,使物块在木板上做匀加速直线运动.(重力加速度为g,滑轮的质量和摩擦可以忽略) 如图所示,实线OD与x轴夹角为θ=37°,在实线OD与y轴之间的范围内有电场强度方向沿y轴负方向的匀强电场,在圆O1对应的圆弧$\widehat{BD}$与线段BD所围的空间内存在方向垂直xoy平面向外的匀强磁场(未画出),一带正电的粒子从y轴上的A点以某一初速度垂直y轴射入电场,然后从B点进入磁场,到达x轴上的C点(C点存在磁场,图中没有标出)时速度方向与x轴垂直.已知$\overline{OA}$=$\overline{OB}$,粒子在磁场中的运动的周期为T、轨道半径为R,不计重力和空气阻力.
如图所示,实线OD与x轴夹角为θ=37°,在实线OD与y轴之间的范围内有电场强度方向沿y轴负方向的匀强电场,在圆O1对应的圆弧$\widehat{BD}$与线段BD所围的空间内存在方向垂直xoy平面向外的匀强磁场(未画出),一带正电的粒子从y轴上的A点以某一初速度垂直y轴射入电场,然后从B点进入磁场,到达x轴上的C点(C点存在磁场,图中没有标出)时速度方向与x轴垂直.已知$\overline{OA}$=$\overline{OB}$,粒子在磁场中的运动的周期为T、轨道半径为R,不计重力和空气阻力.