Question

10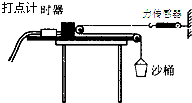．如图所示是测量物块与木板间动摩擦因数的实验装置．长木板固定在水平桌面上，打点计时器固定在长木板上，纸带穿过打点计时器，与带滑轮的物块相连．沙桶和力传感器通过绕在滑轮上的细绳相连．调整沙桶的质量，当放开沙桶时，使物块在木板上做匀加速直线运动．（重力加速度为g，滑轮的质量和摩擦可以忽略）
（1）在某次测量中读出力传感器示数为F，为进一步测量动摩擦因数，下列物理量中还需测量的有BD；
A．木板的长度L   B．物块的质量m      C．沙桶的质量M     D．运动的加速度a
（2）现在已求得物块的加速度为a，利用测得的物理量写出动摩擦因数的表达式μ=$\frac{2F-ma}{mg}$
（3）为使实验结果更精确，该同学改变沙桶的质量，重复以上实验操作，得到多组数据，以力传感器的示数F为横轴，以加速度a为纵轴建立直角坐标系，做出a-F图象，得到一条倾斜的直线，该直线的纵轴截距大小为b，当地的重力加速度g，则由图象可得动摩擦因数μ=$\frac{b}{g}$．

Answer 1

分析 （1）（2）根据实验原理与实验数据，求出动摩擦因数的表达式，从而知需要测量的物理量．
（3）对物块，由牛顿第二定律得：2F-μmg=ma，化简得：a=$\frac{2F}{m}$-μg，结合线性方程判断斜率的值

解答 解：（1）由纸带可以求出物块的加速度a，对物块，由牛顿第二定律得：
2F-μmg=ma，
则动摩擦因数为：μ=$\frac{2F-ma}{mg}$，需要知道加速度a和小车质量m，故选：BD．
（2）由（2）可知，动摩擦因数的表达式为：μ=$\frac{2F-ma}{mg}$．
（3）对物块，由牛顿第二定律得：2F-μmg=ma，
解得：a=$\frac{2F}{m}$-μg，
则图象的截距为：μg=b，所以有：μ=$\frac{b}{g}$
故答案为：（1）BD；（2）$μ=\frac{2F-ma}{mg}$；（3）$\frac{b}{g}$

点评 本题考查测量动摩擦因数涉及牛顿第二定律、加速度的计算及利用图象求解相关物理量等，意在考查学生的综合分析能力，有一定的难度