题目内容
12. 如图,带电量均为+q的一对点电荷,被分别固定在空间相距2h的A、B两点.在正电荷的电场区域内,有一个电子(电量为e,质量为m,重力可不计)正在做匀速圆周运动.设此时电子到正电荷的距离为x,则该电子受到的电场力为$\frac{2kqe\sqrt{{x}^{2}-{h}^{2}}}{{x}^{3}}$,电子的动能Ek与距离x的函数关系为Ek=$\frac{2kqe({x}^{2}-{h}^{2})}{{x}^{3}}$.
如图,带电量均为+q的一对点电荷,被分别固定在空间相距2h的A、B两点.在正电荷的电场区域内,有一个电子(电量为e,质量为m,重力可不计)正在做匀速圆周运动.设此时电子到正电荷的距离为x,则该电子受到的电场力为$\frac{2kqe\sqrt{{x}^{2}-{h}^{2}}}{{x}^{3}}$,电子的动能Ek与距离x的函数关系为Ek=$\frac{2kqe({x}^{2}-{h}^{2})}{{x}^{3}}$.
分析 负点电荷将绕O点在AB的中垂面里做匀速圆周运动,合外力提供向心力,根据向心力公式结合库仑定律以及几何关系求解即可.
解答  解:由题意可知,负点电荷将绕O点在AB的中垂面里做匀速圆周运动,其受力图如图所示,其向心力为:
解:由题意可知,负点电荷将绕O点在AB的中垂面里做匀速圆周运动,其受力图如图所示,其向心力为:
Fn=2Fcosθ=$m\frac{{v}^{2}}{r}$,
根据库仑定律得:F=$\frac{kqe}{{x}^{2}}$
根据几何关系得:cosθ=$\frac{r}{x}=\frac{\sqrt{{x}^{2}-{h}^{2}}}{x}$
解得:Fn=$\frac{2kqe\sqrt{{x}^{2}-{h}^{2}}}{{x}^{3}}$,Ek=$\frac{1}{2}m{v}^{2}$=$\frac{2kqe({x}^{2}-{h}^{2})}{{x}^{3}}$
故答案为:$\frac{2kqe\sqrt{{x}^{2}-{h}^{2}}}{{x}^{3}}$,$\frac{2kqe({x}^{2}-{h}^{2})}{{x}^{3}}$
点评 本题主要考查了向心力公式、库仑定律的直接应用,要求同学们能正确分析电荷的受力情况,找出向心力的来源,注意几何关系在解题中的应用,难度适中.

练习册系列答案
相关题目
12. 在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( )
在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( )
 在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( )
在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( )| A. | 电源的输出功率增大 | B. | A灯和B灯都变亮 | ||
| C. | A灯变亮,B灯变暗 | D. | 电源的工作效率降低 |
20.甲、乙、丙、丁四位同学在做探究加速度与物体质量和合外力的关系的实验时(使用如图所示的装置),设小车质量和车上砝码质量之和为 M,砂及砂桶的总质量为 m,分别得出如图甲、乙、丙、丁四条图线,其中图甲、乙、丙是 a-F 图线,图丁是 a-$\frac{1}{M}$图线,则下列说法中正确的是( )


| A. | 甲和乙较好地把握了实验条件 M 远大于 m | |
| B. | 丙和丁没有把握好实验条件 M 远大于 m | |
| C. | 甲同学长木板的倾角太小,而乙同学长木板倾角太大 | |
| D. | 甲、乙、丙三同学中,丙同学较好地完成了平衡摩擦力的操作 |
 为了“探究外力做功与物体动能变化的关系”,查资料得知,弹簧的弹性势能Ep=$\frac{1}{2}$kx2,其中k是弹簧的劲度系数,x是弹簧长度的变化量.某同学就设想用压缩的弹簧推静止的小球(质量为m)运动来探究这一问题.为了研究方便,把小球放在水平桌面上做实验,让小球在弹力作用下运动,既只有弹簧弹力做功.该同学设计实验如下:
为了“探究外力做功与物体动能变化的关系”,查资料得知,弹簧的弹性势能Ep=$\frac{1}{2}$kx2,其中k是弹簧的劲度系数,x是弹簧长度的变化量.某同学就设想用压缩的弹簧推静止的小球(质量为m)运动来探究这一问题.为了研究方便,把小球放在水平桌面上做实验,让小球在弹力作用下运动,既只有弹簧弹力做功.该同学设计实验如下: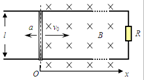 如图所示,两条互相平行且足够长的光滑金属导轨位于水平面内,导轨间距l=0.2m,在导轨的一端接有阻值R=3Ω的电阻,在x≥0处有一垂直导轨平面向里的匀强磁场,磁感强度B=0.5T.一质量m=0.1kg,电阻r=2Ω的金属棒垂直搁在导轨上,并以v0=20m/s的初速度进入磁场,在水平拉力F的作用下作持续的匀变速直线运动,加速度大小a=2m/s2、方向与初速度方向相反.棒与导轨接触良好,其余电阻均不计.求:
如图所示,两条互相平行且足够长的光滑金属导轨位于水平面内,导轨间距l=0.2m,在导轨的一端接有阻值R=3Ω的电阻,在x≥0处有一垂直导轨平面向里的匀强磁场,磁感强度B=0.5T.一质量m=0.1kg,电阻r=2Ω的金属棒垂直搁在导轨上,并以v0=20m/s的初速度进入磁场,在水平拉力F的作用下作持续的匀变速直线运动,加速度大小a=2m/s2、方向与初速度方向相反.棒与导轨接触良好,其余电阻均不计.求: 在纸平面上有一长为h的光滑绝缘空心细管MN,管的M端内有一带正电的小球P1,在纸平面上N端的正右前方2h处有一个不带电的小球P2,开始时P1相对管静止,管水平速度v1,小球P2在纸平面上沿着以于MN延长线方向成45°角的速度v2运动.设管的质量远大于P1的质量,P1在管内的运动对管的运动的影响可以忽略(不计两小球的重力).已知P1离开N端时相对纸面的速度大小恰好为$\sqrt{2}$v1,且在离开管后最终能与P2相碰,空间存在磁感应强度为B的匀强磁场,方向垂直于纸面向里.试求:
在纸平面上有一长为h的光滑绝缘空心细管MN,管的M端内有一带正电的小球P1,在纸平面上N端的正右前方2h处有一个不带电的小球P2,开始时P1相对管静止,管水平速度v1,小球P2在纸平面上沿着以于MN延长线方向成45°角的速度v2运动.设管的质量远大于P1的质量,P1在管内的运动对管的运动的影响可以忽略(不计两小球的重力).已知P1离开N端时相对纸面的速度大小恰好为$\sqrt{2}$v1,且在离开管后最终能与P2相碰,空间存在磁感应强度为B的匀强磁场,方向垂直于纸面向里.试求:
