题目内容
4.在“探究恒力做功与动能改变间的关系”实验中,采用图1所示装置的实验方案,实验时:
(1)若用砂和小桶的总重力表示小车受到的合力,为了减少这种做法带来的实验误差,必须:①使长木板左端抬起一个合适的角度,以平衡摩擦力;
②满足条件,小车质量远大于砂和小桶的总质量(选填“远大于”、“远小于”、“等于”);
③使拉动小车的细线(小车-滑轮段)与长木板平行.
(2)要验证合外力做功与动能变化间的关系,除了要测量砂和小砂桶的总重力、测量小车的位移、速度外,还要测出的物理量有小车质量;如图2所示是某次实验中得到的一条纸带,其中A、B、C、D、E、F是计数点,相邻计数点间的时间间隔为T,距离如图2所示,则打C点时小车的速度vc表达式为(用题中所给物理量表示)${v}_{C}^{\;}=\frac{{s}_{2}^{\;}+{s}_{3}^{\;}}{2T}$.
(3)若已知小车质量为M、砂和小砂桶的总质量为m,打B、E点时小车的速度分别vB、vE,重力加速度为g,探究B到E过程合外力做功与动能变化间的关系,其验证的数学表达式为$mg({s}_{2}^{\;}+{s}_{3}^{\;}+{s}_{4}^{\;})=\frac{1}{2}M{v}_{E}^{2}-\frac{1}{2}M{v}_{B}^{2}$.(用M、m、g、s1~s5、vB、vE表示)
分析 (1)根据实验的原理即可正确解答;
(2)为了使“沙和沙桶的总重力表示小车受到的合外力”所采取措施与验证牛顿第二定律类似;根据动能定理的表达式,即可明确所测物理量.
(3)根据“探究加速度与力、质量的关系”实验原理结合图象特点即可正确回答.
解答 解:(1)若用砂和小桶的总重力表示小车受到的合力,为了减少这种做法带来的实验误差,必须:
①使长木板左端抬起-个合适的角度,以平衡摩擦力,以保证合外力等于绳子的拉力;
②满足条件,小车质量 远大于砂和小桶的总质量,以保证绳子的拉力等于沙与小桶的总重力;
③使拉动小车的细线(小车---滑轮段)与长木板平行,以保证合外力等于绳子的拉力.
(2)根据匀变速直线运动的特点,C点的速度等于BD之间的平均速度,所以:${v}_{C}^{\;}=\frac{{s}_{2}^{\;}+{s}_{3}^{\;}}{2T}$
平衡摩擦力后,小车受到的合力为mg,合外力的功等于动能的变化,因此需要验证的表达式为:mgs=$\frac{1}{2}$MvB2-$\frac{1}{2}$MvA2;
故还需要测出的物理量是小车的质量.
(3)B到E之间重力势能减小为:△EP=mg(s2+s3+s4)
动能增大:$△{E}_{k}^{\;}$=$\frac{1}{2}M{v}_{E}^{2}-\frac{1}{2}M{v}_{B}^{2}$
所以需要验证的是:$mg({s}_{2}^{\;}+{s}_{3}^{\;}+{s}_{4}^{\;})=\frac{1}{2}M{v}_{E}^{2}-\frac{1}{2}M{v}_{B}^{2}$
故答案为:(1)平衡摩擦力,远大于,平行;(2)小车质量,${v}_{C}^{\;}=\frac{{s}_{2}^{\;}+{s}_{3}^{\;}}{2T}$;(3)$mg({s}_{2}^{\;}+{s}_{3}^{\;}+{s}_{4}^{\;})=\frac{1}{2}M{v}_{E}^{2}-\frac{1}{2}M{v}_{B}^{2}$
点评 “探究恒力做功与动能改变的关系”与“探究加速度与力、质量的关系”有很多类似之处,在平时学习中要善于总结、比较,提高对实验的理解能力.

 如图所示,长为L的细绳一端拴一质量为m小球,另一端固定在O点,绳的最大承受能力为11mg,在O点正下方O′点有一小钉,先把绳拉至水平再释放小球,为使绳不被拉断且小球能以O′为轴完成竖直面完整的圆周运动,则钉的位置到O点的距离为( )
如图所示,长为L的细绳一端拴一质量为m小球,另一端固定在O点,绳的最大承受能力为11mg,在O点正下方O′点有一小钉,先把绳拉至水平再释放小球,为使绳不被拉断且小球能以O′为轴完成竖直面完整的圆周运动,则钉的位置到O点的距离为( )| A. | 最小为$\frac{2}{5}$L | B. | 最小为$\frac{3}{5}$L | C. | 最大为$\frac{4}{5}$L | D. | 最大为$\frac{9}{10}$L |
 在光滑绝缘水平面上,一轻绳拉着一个带电小球绕竖直方向的轴O在匀强磁场中做逆时针方向的匀速圆周运动,磁场方向竖直向下,且范围足够大,其俯视图如图所示,若小球运动到某点时,绳子突然断开,则关于绳子断开后,对小球可能的运动情况的判断不正确的是( )
在光滑绝缘水平面上,一轻绳拉着一个带电小球绕竖直方向的轴O在匀强磁场中做逆时针方向的匀速圆周运动,磁场方向竖直向下,且范围足够大,其俯视图如图所示,若小球运动到某点时,绳子突然断开,则关于绳子断开后,对小球可能的运动情况的判断不正确的是( )| A. | 小球做顺时针方向的匀速圆周运动,半径不变 | |
| B. | 小球仍做逆时针方向的匀速圆周运动,半径不变 | |
| C. | 小球仍做逆时针方向的匀速圆周运动,但半径减小 | |
| D. | 小球做顺时针方向的匀速圆周运动,半径减小 |
 在反恐演习中,中国特种兵进行了飞行跳伞表演,伞兵从静止的直升机跳下且竖直下落,在t0时刻打开降落伞,在3t0时刻以v2速度着地,伞兵运动的速度时间图象如图所示下列结论中正确的是( )
在反恐演习中,中国特种兵进行了飞行跳伞表演,伞兵从静止的直升机跳下且竖直下落,在t0时刻打开降落伞,在3t0时刻以v2速度着地,伞兵运动的速度时间图象如图所示下列结论中正确的是( )| A. | 在0~t0时间内加速度一直增大 | |
| B. | 在t0~3t0之间加速度一直减小 | |
| C. | 在t0~3t0时间内平均速度$\overline{v}$<$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| D. | 若第一个伞兵在空中打开降落伞时第二个伞兵立即跳下则他们在空中的距离先增大后减小 |
 某实验小组用如图所示实验装置探究合力做功与动能变化的关系,铁架台竖直固定放置在水平桌面上,长木板一端放置在水平桌面边缘P处,另一位置放置在铁架台竖直铁杆上,使长木板倾斜放置.长木板P处放置一光电门,用光电计时器记录滑块通过光电门时挡光时间,实验步骤是:
某实验小组用如图所示实验装置探究合力做功与动能变化的关系,铁架台竖直固定放置在水平桌面上,长木板一端放置在水平桌面边缘P处,另一位置放置在铁架台竖直铁杆上,使长木板倾斜放置.长木板P处放置一光电门,用光电计时器记录滑块通过光电门时挡光时间,实验步骤是: 如图,带电量均为+q的一对点电荷,被分别固定在空间相距2h的A、B两点.在正电荷的电场区域内,有一个电子(电量为e,质量为m,重力可不计)正在做匀速圆周运动.设此时电子到正电荷的距离为x,则该电子受到的电场力为$\frac{2kqe\sqrt{{x}^{2}-{h}^{2}}}{{x}^{3}}$,电子的动能Ek与距离x的函数关系为Ek=$\frac{2kqe({x}^{2}-{h}^{2})}{{x}^{3}}$.
如图,带电量均为+q的一对点电荷,被分别固定在空间相距2h的A、B两点.在正电荷的电场区域内,有一个电子(电量为e,质量为m,重力可不计)正在做匀速圆周运动.设此时电子到正电荷的距离为x,则该电子受到的电场力为$\frac{2kqe\sqrt{{x}^{2}-{h}^{2}}}{{x}^{3}}$,电子的动能Ek与距离x的函数关系为Ek=$\frac{2kqe({x}^{2}-{h}^{2})}{{x}^{3}}$.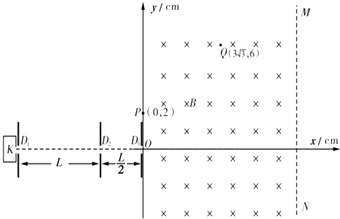 如图所示,K是粒子发生器,D1、D2、D3是三块挡板,通过传感器可控制它们定时开启和关闭,D1、D2的间距为L,D2、D3的间距为$\frac{L}{2}$.在以O为原点的直角坐标系Oxy中有一磁感应强度大小为B,方向垂直纸面向里的匀强磁场,y轴和直线MN是它的左、右边界,且MN平行于y轴.现开启挡板D1、D3,粒子发生器仅在t=0时刻沿x轴正方向发射各种速率的粒子,D2仅在t=nT(n=0,1,2…,T为周期)时刻开启,在t=5T时刻,再关闭挡板D3,使粒子无法进入磁场区域.已知挡板的厚度不计,粒子质量为m、电荷量为+q(q大于0),不计粒子的重力,不计粒子间的相互作用,整个装置都放在真空中.
如图所示,K是粒子发生器,D1、D2、D3是三块挡板,通过传感器可控制它们定时开启和关闭,D1、D2的间距为L,D2、D3的间距为$\frac{L}{2}$.在以O为原点的直角坐标系Oxy中有一磁感应强度大小为B,方向垂直纸面向里的匀强磁场,y轴和直线MN是它的左、右边界,且MN平行于y轴.现开启挡板D1、D3,粒子发生器仅在t=0时刻沿x轴正方向发射各种速率的粒子,D2仅在t=nT(n=0,1,2…,T为周期)时刻开启,在t=5T时刻,再关闭挡板D3,使粒子无法进入磁场区域.已知挡板的厚度不计,粒子质量为m、电荷量为+q(q大于0),不计粒子的重力,不计粒子间的相互作用,整个装置都放在真空中.
 某个小组的三位同学按照正确的操作得到的纸带如图所示,其中O是起始点,A、B、C是打点计时器连续打下的3个点,该同学用毫米刻度尺测量O到A、B、C各点的距离,用重锤在OB段的运动来验证机械能守恒,已知当地的重力加速度g=9.80m/s2,打点计时器所用电源频率为f=50Hz,设重锤质量为1.00kg.
某个小组的三位同学按照正确的操作得到的纸带如图所示,其中O是起始点,A、B、C是打点计时器连续打下的3个点,该同学用毫米刻度尺测量O到A、B、C各点的距离,用重锤在OB段的运动来验证机械能守恒,已知当地的重力加速度g=9.80m/s2,打点计时器所用电源频率为f=50Hz,设重锤质量为1.00kg.