题目内容
9. 如图所示,一辆质量为4t的汽车匀速经过一半径为50m的凸形桥.(g=10m/s2)
如图所示,一辆质量为4t的汽车匀速经过一半径为50m的凸形桥.(g=10m/s2)(1)汽车若能安全驶过此桥,它在桥顶的最大速度不应超过为多少?
(2)若汽车经最高点时对桥的压力等于它重力的一半,求此时汽车的速度多大?
分析 (1)当小车对桥无压力时,汽车速度最大,此时只受重力,重力恰好提供向心力.
(2)在最高点,根据合外力提供向心力列式即可求解.
解答 解:(1)汽车经最高点时对桥的压力为零时,求出速度最大,此时重力提供向心力,则有:
mg=m$\frac{{v}^{2}}{R}$
解得:v=$\sqrt{gR}=10\sqrt{5}m/s$
(2)汽车经最高点时对桥的压力等于它重力的一半时,根据合外力提供向心力由于:
mg-$\frac{1}{2}mg=m\frac{v{′}^{2}}{R}$
解得:v′=$\sqrt{\frac{1}{2}gR}=5\sqrt{10}m/s$
答:(1)汽车若能安全驶过此桥,它在桥顶的最大速度不应超过$10\sqrt{5}m/s$;
(2)若汽车经最高点时对桥的压力等于它重力的一半,此时汽车的速度为$5\sqrt{5}m/s$.
点评 本题关键对物体进行运动情况分析和受力情况分析,然后根据向心力公式列式求解!

练习册系列答案
相关题目
4. 热现象与大量分子热运动的统计规律有关,1859年麦克斯韦从理论上推导出了气体分子速率的分布规律,后来有许多实验验证了这一规律.若以横坐标v表示分子速率,纵坐标f(v)表示各速率区间的分子数占总分子数的百分比.对某一部分密闭在钢瓶中的理想气体,在温度T1、T2时的分子速率分布图象如题图所示,下列分析和判断中正确的是( )
热现象与大量分子热运动的统计规律有关,1859年麦克斯韦从理论上推导出了气体分子速率的分布规律,后来有许多实验验证了这一规律.若以横坐标v表示分子速率,纵坐标f(v)表示各速率区间的分子数占总分子数的百分比.对某一部分密闭在钢瓶中的理想气体,在温度T1、T2时的分子速率分布图象如题图所示,下列分析和判断中正确的是( )
 热现象与大量分子热运动的统计规律有关,1859年麦克斯韦从理论上推导出了气体分子速率的分布规律,后来有许多实验验证了这一规律.若以横坐标v表示分子速率,纵坐标f(v)表示各速率区间的分子数占总分子数的百分比.对某一部分密闭在钢瓶中的理想气体,在温度T1、T2时的分子速率分布图象如题图所示,下列分析和判断中正确的是( )
热现象与大量分子热运动的统计规律有关,1859年麦克斯韦从理论上推导出了气体分子速率的分布规律,后来有许多实验验证了这一规律.若以横坐标v表示分子速率,纵坐标f(v)表示各速率区间的分子数占总分子数的百分比.对某一部分密闭在钢瓶中的理想气体,在温度T1、T2时的分子速率分布图象如题图所示,下列分析和判断中正确的是( )| A. | 两种状态下瓶中气体内能相等 | |
| B. | 两种状态下瓶中气体分子平均动能相等 | |
| C. | 两种状态下瓶中气体分子势能相等 | |
| D. | 两种状态下瓶中气体分子单位时间内撞击瓶壁的总冲量相等 |
1.下列说法不正确的是( )
| A. | 核聚变反应方程${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n中,${\;}_{0}^{1}$n表示中子 | |
| B. | 某放射性原子核经过2次α衰变和一次β衰变,核内质子数减少3个 | |
| C. | 太阳内部发生的核反应是热核反应 | |
| D. | 机场、车站等地进行安全检查时,能轻而易举地窥见箱内物品,利用了γ射线较强的穿透能力 |
18. 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )| A. | W1=$\frac{mg}{2h}$(h2-R2) | B. | W2=GR(1-$\frac{R}{h}$) | C. | W1=$\frac{hKQq}{{R}^{2}}$(1-$\frac{R}{h}$) | D. | G=$\frac{khQq}{{R}^{2}}$ |
19. 如图所示,横截面为等腰直角三角形ABC的棱镜,一束绿光从AB面射入,且光在AB面入射角的正弦值为$\frac{\sqrt{3}}{3}$,此绿光恰好在AC面上发生全反射,下列光现象的说法哪个是正确的( )(光在真空中传播速度为c)
如图所示,横截面为等腰直角三角形ABC的棱镜,一束绿光从AB面射入,且光在AB面入射角的正弦值为$\frac{\sqrt{3}}{3}$,此绿光恰好在AC面上发生全反射,下列光现象的说法哪个是正确的( )(光在真空中传播速度为c)
 如图所示,横截面为等腰直角三角形ABC的棱镜,一束绿光从AB面射入,且光在AB面入射角的正弦值为$\frac{\sqrt{3}}{3}$,此绿光恰好在AC面上发生全反射,下列光现象的说法哪个是正确的( )(光在真空中传播速度为c)
如图所示,横截面为等腰直角三角形ABC的棱镜,一束绿光从AB面射入,且光在AB面入射角的正弦值为$\frac{\sqrt{3}}{3}$,此绿光恰好在AC面上发生全反射,下列光现象的说法哪个是正确的( )(光在真空中传播速度为c)| A. | 换成红光沿同一入射光路射到AB面,它在AC面也会全反射 | |
| B. | 绿光在棱镜中的传播速度为$\frac{\sqrt{3}}{2}$c | |
| C. | 棱镜对绿光的折射率为$\sqrt{3}$ | |
| D. | 绿光由空气进入棱镜其波长会变长 |
 如图,在场强大小为E、水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动.杆的两端分别固定两电荷量均为q的小球A、B,A带正电,B带负电;A、B两球到转轴O的距离分别为2l、l,所受重力大小均为电场力大小的$\sqrt{3}$倍.开始时杆与电场间夹角为θ(90°≤θ≤180°).将杆从初始位置由静止释放,以O点为重力势能和电势能零点.求:
如图,在场强大小为E、水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动.杆的两端分别固定两电荷量均为q的小球A、B,A带正电,B带负电;A、B两球到转轴O的距离分别为2l、l,所受重力大小均为电场力大小的$\sqrt{3}$倍.开始时杆与电场间夹角为θ(90°≤θ≤180°).将杆从初始位置由静止释放,以O点为重力势能和电势能零点.求: 如图所示,在直角坐标系O-xyz中存在磁感应强度为B=$\frac{2m}{q}$$\sqrt{\frac{g}{h}}$,方向竖直向下的匀强磁场,在(0,0,h)处固定一电量为+q(q>0)的点电荷,在xOy平面内有一质量为m,电量为-q的微粒绕原点O沿图示方向作匀速圆周运动.若该微粒的圆周运动可以等效为环形电流,求此等效环形电流强度I.(重力加速度为g)
如图所示,在直角坐标系O-xyz中存在磁感应强度为B=$\frac{2m}{q}$$\sqrt{\frac{g}{h}}$,方向竖直向下的匀强磁场,在(0,0,h)处固定一电量为+q(q>0)的点电荷,在xOy平面内有一质量为m,电量为-q的微粒绕原点O沿图示方向作匀速圆周运动.若该微粒的圆周运动可以等效为环形电流,求此等效环形电流强度I.(重力加速度为g) 如图所示为汽车电磁感应减速带原理图(俯视图),在汽车通过的区域设置匀强磁场,其方向垂直地面向上,大小为B,宽度为d.在汽车底部固定有一个长度L1、宽度L2的N匝矩形线圈,线圈的总电阻为R,车和线圈的总质量为m,假设汽车运动过程中所受阻力恒为f.当汽车以初速度v0进入磁场区域的左侧,开始以大小为a的恒定加速度减速驶入磁场区域,线圈全部进入磁场后,立即做匀速直线运动,直至完全离开缓冲区域,已知从线圈刚进入磁场到完全穿出磁场的过程中,汽车的牵引力做的总功为W.从线圈的前边与磁场左边线重合开始计时.求:
如图所示为汽车电磁感应减速带原理图(俯视图),在汽车通过的区域设置匀强磁场,其方向垂直地面向上,大小为B,宽度为d.在汽车底部固定有一个长度L1、宽度L2的N匝矩形线圈,线圈的总电阻为R,车和线圈的总质量为m,假设汽车运动过程中所受阻力恒为f.当汽车以初速度v0进入磁场区域的左侧,开始以大小为a的恒定加速度减速驶入磁场区域,线圈全部进入磁场后,立即做匀速直线运动,直至完全离开缓冲区域,已知从线圈刚进入磁场到完全穿出磁场的过程中,汽车的牵引力做的总功为W.从线圈的前边与磁场左边线重合开始计时.求: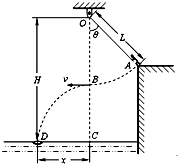 某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,$\sqrt{12.96}$=3.6,g=10m/s2)
某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,$\sqrt{12.96}$=3.6,g=10m/s2)