题目内容
20. 如图所示,在直角坐标系O-xyz中存在磁感应强度为B=$\frac{2m}{q}$$\sqrt{\frac{g}{h}}$,方向竖直向下的匀强磁场,在(0,0,h)处固定一电量为+q(q>0)的点电荷,在xOy平面内有一质量为m,电量为-q的微粒绕原点O沿图示方向作匀速圆周运动.若该微粒的圆周运动可以等效为环形电流,求此等效环形电流强度I.(重力加速度为g)
如图所示,在直角坐标系O-xyz中存在磁感应强度为B=$\frac{2m}{q}$$\sqrt{\frac{g}{h}}$,方向竖直向下的匀强磁场,在(0,0,h)处固定一电量为+q(q>0)的点电荷,在xOy平面内有一质量为m,电量为-q的微粒绕原点O沿图示方向作匀速圆周运动.若该微粒的圆周运动可以等效为环形电流,求此等效环形电流强度I.(重力加速度为g)
分析 对微粒正确受力分析,在竖直方向应用平衡条件、在水平面内应用牛顿第二定律求出微粒做匀速圆周运动的角速度,然后求出微粒做圆周运动的周期,最后根据电流的定义求出等效电流.
解答 解:微粒受力如图所示,电场力:
FE=k$\frac{{q}^{2}}{{R}^{2}}$,
洛伦兹力:FB=qvB,
微粒的线速度:v=ωr,
由几何知识得:r=htanθ,R=$\frac{h}{cosθ}$,
微粒在Z轴方向受力平衡:FEcosθ-mg=0,
微粒在xoy平面内做匀速圆周运动,
由牛顿第二定律得:FEsinθ-FB=mω2r,
解得:ω2+2$\sqrt{\frac{g}{h}}$ω-$\frac{g}{h}$=0,
解得:ω=($\sqrt{2}$-1)$\sqrt{\frac{g}{h}}$[ω=-($\sqrt{2}$+1)$\sqrt{\frac{g}{h}}$不合题意,舍去],
微粒做圆周运动的周期:T=$\frac{2π}{ω}$,
等效电流:I=$\frac{q}{T}$=$\frac{(\sqrt{2}-1)q}{2π}$$\sqrt{\frac{g}{h}}$;
答:等效环形电流强度I为$\frac{(\sqrt{2}-1)q}{2π}$$\sqrt{\frac{g}{h}}$.
点评 本题考查了带电微粒在电场、磁场与重力场中的运动,微粒在z轴方向受力平衡,在xoy面内做匀速圆周运动,应用平衡条件与牛顿第二定律、电流定义式可以解题.

练习册系列答案
相关题目
13.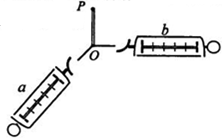 在《互成角度的两个力的合成》这一实验中,如图所示,使b弹簧由图示位置开始缓慢顺时针转动直到接近竖直,在这过程中,保持O点的位置和a弹簧秤的拉伸方向不变,则在整个过程中,关于a、b两弹簧秤示数的变化情况是( )
在《互成角度的两个力的合成》这一实验中,如图所示,使b弹簧由图示位置开始缓慢顺时针转动直到接近竖直,在这过程中,保持O点的位置和a弹簧秤的拉伸方向不变,则在整个过程中,关于a、b两弹簧秤示数的变化情况是( )
 在《互成角度的两个力的合成》这一实验中,如图所示,使b弹簧由图示位置开始缓慢顺时针转动直到接近竖直,在这过程中,保持O点的位置和a弹簧秤的拉伸方向不变,则在整个过程中,关于a、b两弹簧秤示数的变化情况是( )
在《互成角度的两个力的合成》这一实验中,如图所示,使b弹簧由图示位置开始缓慢顺时针转动直到接近竖直,在这过程中,保持O点的位置和a弹簧秤的拉伸方向不变,则在整个过程中,关于a、b两弹簧秤示数的变化情况是( )| A. | a示数增大,b示数增大 | B. | a示数减小,b示数先增大后减小 | ||
| C. | a示数减小,b示数减小 | D. | 示数减小,b示数先减小后增大 |
11.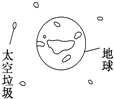 不可回收的航天器在使用后,将成为太空垃圾.如图所示是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )
不可回收的航天器在使用后,将成为太空垃圾.如图所示是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )
 不可回收的航天器在使用后,将成为太空垃圾.如图所示是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )
不可回收的航天器在使用后,将成为太空垃圾.如图所示是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )| A. | 离地越低的太空垃圾运行周期越大 | |
| B. | 离地越高的太空垃圾运行角速度越小 | |
| C. | 由公式v=$\sqrt{gr}$得,离地越高的太空垃圾运行速率越大 | |
| D. | 太空垃圾一定能跟同一轨道上同向飞行的航天器相撞 |
8.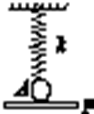 如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )
如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )
 如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )
如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )| A. | 小球与与挡板分离的时间为t=$\sqrt{\frac{ka}{2m(g-a)}}$ | |
| B. | 小球与与挡板分离的时间为t=$\sqrt{\frac{2m(g-a)}{ka}}$ | |
| C. | 小球从开始运动直到最低点的过程中,小球速度最大时弹簧的伸长量x=$\frac{mg}{k}$ | |
| D. | 小球从开始运动直到最低点的过程中,小球速度最大时弹簧的伸长量x=$\frac{m(g-a)}{k}$ |
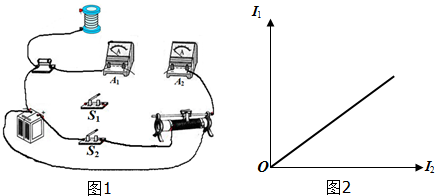
10.如图是街头变压器通过降压给用户供电的示意图.变压器的输入电压是市区电网的电压,假设负载变化时输入电压保持不变.输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,R代表各户用中电器电阻.忽略变压器上的能量损失,不计电压表、电流表的内阻对电路的影响.当用户的用电器增加时,下列说法正确的是( )


| A. | 输出功率变小 | |
| B. | 输入功率不变 | |
| C. | 电压表1读数不变,电流表1读数增大 | |
| D. | 电压表2读数增大,电流表2读数增大 |
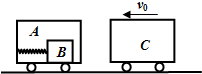 如图所示,质量为2M的小车A静止在光滑水平桌面上,质量为3M的物体B静置于A车车厢内,B左端用轻弹簧与A车连接,弹簧劲度系数为k且水平,处于原长,小车底面光滑.质量为M的小车C以速度v0向小车A滑过去,并在与小车A碰撞后立即与A车粘连,整个过程中B始终不与车厢侧壁碰撞.求之后的运动过程中弹簧的最大长度与最短长度之差.(弹簧弹性势能表达式为Ep=$\frac{1}{2}$kx2,x为弹簧形变量).
如图所示,质量为2M的小车A静止在光滑水平桌面上,质量为3M的物体B静置于A车车厢内,B左端用轻弹簧与A车连接,弹簧劲度系数为k且水平,处于原长,小车底面光滑.质量为M的小车C以速度v0向小车A滑过去,并在与小车A碰撞后立即与A车粘连,整个过程中B始终不与车厢侧壁碰撞.求之后的运动过程中弹簧的最大长度与最短长度之差.(弹簧弹性势能表达式为Ep=$\frac{1}{2}$kx2,x为弹簧形变量). 如图所示,一辆质量为4t的汽车匀速经过一半径为50m的凸形桥.(g=10m/s2)
如图所示,一辆质量为4t的汽车匀速经过一半径为50m的凸形桥.(g=10m/s2)