题目内容
14.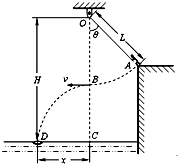 某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,$\sqrt{12.96}$=3.6,g=10m/s2)
某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,$\sqrt{12.96}$=3.6,g=10m/s2)(1)求参赛者经过B点时速度的大小v;
(2)参赛者从台阶上A点跃出时的动能Ek为多大?
分析 (1)人从B向D运动做平抛运动,根据平抛运动的位移公式列式求解即可;
(2)人从A到B过程机械能守恒,根据机械能守恒定律列式求解即可.
解答 解:(1)参赛者从B点到D点做平抛运动,有:
H-L=$\frac{1}{2}g{t}^{2}$…①
x=vBt…②
由①②式得:vB=x$\sqrt{\frac{g}{2(H-L)}}$=4.8×$\sqrt{\frac{10}{2×(10-5)}}$=4.8m/s
(2)参赛者从A点到B点的过程中,由机械能守恒定律得:
mghAB=$\frac{1}{2}m{v}_{B}^{2}$-Ek…③
其中 hAB=L(1-cosθ)…④
由③④式代入数据解得:Ek=76J
答:(1)参赛者经过B点时速度的大小是4.8m/s;
(2)参赛者从台阶上A点跃出时的动能Ek为76J
点评 本题是两个过程的问题,运用平抛运动的规律、机械能守恒或动能定理结合进行研究,只需分析清楚过程即可顺利求解.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
2. 我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
 我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )| A. | $\frac{m{g}_{月}R}{R+h}$(h+2R) | B. | $\frac{m{g}_{月}R}{R+h}$(h+$\sqrt{2}$R) | C. | $\frac{m{g}_{月}R}{R+h}$(h+$\frac{\sqrt{2}}{2}$R) | D. | $\frac{m{g}_{月}R}{R+h}$(h+$\frac{1}{2}$R) |
 如图所示,一辆质量为4t的汽车匀速经过一半径为50m的凸形桥.(g=10m/s2)
如图所示,一辆质量为4t的汽车匀速经过一半径为50m的凸形桥.(g=10m/s2)
 一长度为l的不可伸长的轻质细绳下端系一质量为m可视为质点的小球,如图所示在水平面内做匀速圆周运动,细线和竖直方向的夹角θ=53°,求:(取sin37°=0.60,cos37°=0.80)
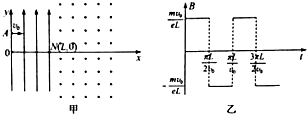
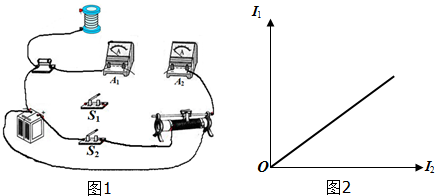
一长度为l的不可伸长的轻质细绳下端系一质量为m可视为质点的小球,如图所示在水平面内做匀速圆周运动,细线和竖直方向的夹角θ=53°,求:(取sin37°=0.60,cos37°=0.80) 在地面附近的真空中,存在着竖直向上的匀强电场和垂直电场方向水平向里的匀强磁场,如图甲所示.磁场的磁感应强度B(图象中的B0末知)随时间t的变化情况如图乙所示.该区域中有一条水平直线MN,D是MN上的一点.在t=0时刻,有一个质量为m、电荷量为+q的小球(可看做质点),从M点开始沿着水平直线以速度v0向右做匀速直线运动,t0时刻恰好到达N点.经观测发现,小球在t=2t0至t=3t0时间内的某一时刻,又竖直向下经过直线MN上的D点,并且以后小球多次水平向右或竖直向下经过D点.不考虑地磁场的影响,求:
在地面附近的真空中,存在着竖直向上的匀强电场和垂直电场方向水平向里的匀强磁场,如图甲所示.磁场的磁感应强度B(图象中的B0末知)随时间t的变化情况如图乙所示.该区域中有一条水平直线MN,D是MN上的一点.在t=0时刻,有一个质量为m、电荷量为+q的小球(可看做质点),从M点开始沿着水平直线以速度v0向右做匀速直线运动,t0时刻恰好到达N点.经观测发现,小球在t=2t0至t=3t0时间内的某一时刻,又竖直向下经过直线MN上的D点,并且以后小球多次水平向右或竖直向下经过D点.不考虑地磁场的影响,求: