��Ŀ����
18�� ��ͼ��ʾ���ڹ⻬С����C���·����h��A���̶�һ����ΪQ�ĵ��ɣ�����Ϊq�Ĵ���С��B���þ�Եϸ��˩�ţ�ϸ�߿�������֣���һ�����ʵ���С������ס��ʹС���ھ�ֹ״̬����ʱС����A��ľ���ΪR��ϸ��CB��AB��ֱ��������������ΪK����������Ϊ��գ�����С�����ܵ�������ΪG����������ϸ�ߣ�ʼ�ձ���С��ƽ�⣩ֱ��С��յ����ֵ����·������У����������Ĺ�ΪW1���糡������ΪW2�������й�ϵʽ��ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬С����C���·����h��A���̶�һ����ΪQ�ĵ��ɣ�����Ϊq�Ĵ���С��B���þ�Եϸ��˩�ţ�ϸ�߿�������֣���һ�����ʵ���С������ס��ʹС���ھ�ֹ״̬����ʱС����A��ľ���ΪR��ϸ��CB��AB��ֱ��������������ΪK����������Ϊ��գ�����С�����ܵ�������ΪG����������ϸ�ߣ�ʼ�ձ���С��ƽ�⣩ֱ��С��յ����ֵ����·������У����������Ĺ�ΪW1���糡������ΪW2�������й�ϵʽ��ȷ���ǣ�������| A�� | W1=$\frac{mg}{2h}$��h2-R2�� | B�� | W2=GR��1-$\frac{R}{h}$�� | C�� | W1=$\frac{hKQq}{{R}^{2}}$��1-$\frac{R}{h}$�� | D�� | G=$\frac{khQq}{{R}^{2}}$ |
���� ��С����B���������������ֽ⣬����������С��
�����ƶ����̿���Ϊ�ٶ�ʼ��Ϊ0��ԭ����˵��ĩλ���ڻ����·�����������ȷ����С������������Ӧ�����������ƿ�ȷ��ĩλ�ã��ٶ��ƶ�����ʹ�ö��ܶ���������������Ĺ���
��� �⣺��С����B��ʱ������������ͼ
��$F=G\;sin��=\frac{kQq}{{R}^{2}}$
���$G=\frac{hKQq}{{R}^{3}}$
��С���ƶ����̣����ڡ�ABC�ס�BED����ͼ��
��С���ƶ�ʱ������F��G���䣬���AB��AC���Ȳ��䣬����С��ͣ��A���Ϸ�����ΪR��H����ͼ
��ȫ���̿�����F��������ȫ�����ɶ��ܶ�����
-GR��1-sin����+W1=0
���${W}_{1}=GR��1-\frac{R}{h}��$����$G=\frac{hKQq}{{R}^{3}}$����Ҳ��д��${W}_{1}=\frac{hKQq}{{R}^{2}}��1-\frac{R}{h}��$
��ѡ��C
���� ���⿼�鶯�ܶ����������������������ƽ�⡢����Ķ�̬ƽ������⣬�õ�ʸ����������ʵ�����������Ƶ�ԭ�����������뵽���ѶȽϴ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
8��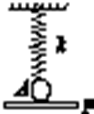 ��ͼ��ʾ������ϵ��Ϊk���ᵯ���¶�ϵһ������Ϊm��С��A��С��ˮƽ����P��סʹ���ɳ���ǡΪ��Ȼ���ȣ�С���뵲�岻ճ������Ȼ��ʹ����P�Ժ㶨�ļ��ٶ�a��a��g����ʼ��ֱ�������ȼ���ֱ���˶���������
��ͼ��ʾ������ϵ��Ϊk���ᵯ���¶�ϵһ������Ϊm��С��A��С��ˮƽ����P��סʹ���ɳ���ǡΪ��Ȼ���ȣ�С���뵲�岻ճ������Ȼ��ʹ����P�Ժ㶨�ļ��ٶ�a��a��g����ʼ��ֱ�������ȼ���ֱ���˶���������
 ��ͼ��ʾ������ϵ��Ϊk���ᵯ���¶�ϵһ������Ϊm��С��A��С��ˮƽ����P��סʹ���ɳ���ǡΪ��Ȼ���ȣ�С���뵲�岻ճ������Ȼ��ʹ����P�Ժ㶨�ļ��ٶ�a��a��g����ʼ��ֱ�������ȼ���ֱ���˶���������
��ͼ��ʾ������ϵ��Ϊk���ᵯ���¶�ϵһ������Ϊm��С��A��С��ˮƽ����P��סʹ���ɳ���ǡΪ��Ȼ���ȣ�С���뵲�岻ճ������Ȼ��ʹ����P�Ժ㶨�ļ��ٶ�a��a��g����ʼ��ֱ�������ȼ���ֱ���˶���������| A�� | С�����뵲������ʱ��Ϊt=$\sqrt{\frac{ka}{2m��g-a��}}$ | |
| B�� | С�����뵲������ʱ��Ϊt=$\sqrt{\frac{2m��g-a��}{ka}}$ | |
| C�� | С��ӿ�ʼ�˶�ֱ����͵�Ĺ����У�С���ٶ����ʱ���ɵ��쳤��x=$\frac{mg}{k}$ | |
| D�� | С��ӿ�ʼ�˶�ֱ����͵�Ĺ����У�С���ٶ����ʱ���ɵ��쳤��x=$\frac{m��g-a��}{k}$ |
10����ͼ�ǽ�ͷ��ѹ��ͨ����ѹ���û������ʾ��ͼ����ѹ���������ѹ�����������ĵ�ѹ�����踺�ر仯ʱ�����ѹ���ֲ��䣮�����ѹͨ������������û�����������ߵ��ܵ�����R0��ʾ��R�����������е������裮���Ա�ѹ���ϵ�������ʧ�����Ƶ�ѹ����������������Ե�·��Ӱ�죮���û����õ�������ʱ������˵����ȷ���ǣ�������


| A�� | ������ʱ�С | |
| B�� | ���빦�ʲ��� | |
| C�� | ��ѹ��1�������䣬������1�������� | |
| D�� | ��ѹ��2������������2�������� |
7������˵������ȷ���У�������
| A�� | ���ܹ�Դ��۲����Ƿ��������˶����۲��߹۲쵽�Ĺ����Dz���� | |
| B�� | ˮ���ϵ���Ĥ���ֲ�ɫ�ǹ�ĸ������� | |
| C�� | �ڹ��ά���ڴ���ͼ�������ù��ɫɢ���� | |
| D�� | ��Դ��ֹ�Ĺ۲����˶����۲��߽��յ���Ƶ��С����Դ��Ƶ�� | |
| E�� | δ��������������������Ϊ���������ϳ����������������� |
 ��ͼ��ʾ��һ������Ϊ4t���������پ���һ�뾶Ϊ50m�����ţ���g=10m/s2��
��ͼ��ʾ��һ������Ϊ4t���������پ���һ�뾶Ϊ50m�����ţ���g=10m/s2�� һ����Ϊl�IJ����쳤������ϸ���¶�ϵһ����Ϊm����Ϊ�ʵ��С����ͼ��ʾ��ˮƽ����������Բ���˶���ϸ�ߺ���ֱ����ļнǦ�=53�㣬��ȡsin37��=0.60��cos37��=0.80��
һ����Ϊl�IJ����쳤������ϸ���¶�ϵһ����Ϊm����Ϊ�ʵ��С����ͼ��ʾ��ˮƽ����������Բ���˶���ϸ�ߺ���ֱ����ļнǦ�=53�㣬��ȡsin37��=0.60��cos37��=0.80��
 �ڵ��渽��������У���������ֱ���ϵ���ǿ�糡�ʹ�ֱ�糡����ˮƽ�������ǿ�ų�����ͼ����ʾ���ų��ĴŸ�Ӧǿ��B��ͼ���е�B0ĩ֪����ʱ��t�ı仯�����ͼ����ʾ������������һ��ˮƽֱ��MN��D��MN�ϵ�һ�㣮��t=0ʱ�̣���һ������Ϊm�������Ϊ+q��С�ɿ����ʵ㣩����M�㿪ʼ����ˮƽֱ�����ٶ�v0����������ֱ���˶���t0ʱ��ǡ�õ���N�㣮���۲ⷢ�֣�С����t=2t0��t=3t0ʱ���ڵ�ijһʱ�̣�����ֱ���¾���ֱ��MN�ϵ�D�㣬�����Ժ�С����ˮƽ���һ���ֱ���¾���D�㣮�����ǵشų���Ӱ�죬��
�ڵ��渽��������У���������ֱ���ϵ���ǿ�糡�ʹ�ֱ�糡����ˮƽ�������ǿ�ų�����ͼ����ʾ���ų��ĴŸ�Ӧǿ��B��ͼ���е�B0ĩ֪����ʱ��t�ı仯�����ͼ����ʾ������������һ��ˮƽֱ��MN��D��MN�ϵ�һ�㣮��t=0ʱ�̣���һ������Ϊm�������Ϊ+q��С�ɿ����ʵ㣩����M�㿪ʼ����ˮƽֱ�����ٶ�v0����������ֱ���˶���t0ʱ��ǡ�õ���N�㣮���۲ⷢ�֣�С����t=2t0��t=3t0ʱ���ڵ�ijһʱ�̣�����ֱ���¾���ֱ��MN�ϵ�D�㣬�����Ժ�С����ˮƽ���һ���ֱ���¾���D�㣮�����ǵشų���Ӱ�죬��