题目内容
9.某同学质量为60kg,在军事训练中要求他从岸上以大小为2m/s的速度跳到一条向他缓慢飘来的小船上,然后去执行任务,小船的质量是140kg,原来的速度大小是0.5m/s,该同学上船后又跑了几步,最终停在船上,则( )| A. | 该过程同学的动量变化量为105m/s | B. | 船最终的速度是0.95m/s | ||
| C. | 人和小船最终静止在水面上 | D. | 船的动量变化量是70m/s |
分析 水的阻力忽略不计,该同学跳上小船后与小船达到同一速度的过程,人和船组成的系统合外力为零,系统的动量守恒,根据动量守恒定律列式求解.
解答 解:BC、该同学与船组成的系统动量守恒,以人的初速度方向为正方向,由动量守恒定律得:m人v人-m船v船=(m人+m船)v
解得:v=0.25m/s,故BC错误;
A、该同学动量变化量:△p=m人v-m人v人=60×0.25-60×2=-105kg•m/s,负号表示动量变化量的方向与初动量方向相反,故A正确;
D、船的动量变化量为:△p′=m船v-m船v船=140×0.25-140×(-0.5)=105kg•m/s,故D错误;
故选:A.
点评 解答本题的关键是抓住已知条件,判断人和船系统的动量守恒,同时要注意选取正方向,用符号表示速度的方向.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图所示,斜劈劈尖顶着竖直墙壁静止与水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )
如图所示,斜劈劈尖顶着竖直墙壁静止与水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )
 如图所示,斜劈劈尖顶着竖直墙壁静止与水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )
如图所示,斜劈劈尖顶着竖直墙壁静止与水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )| A. | 斜劈对小球的弹力做负功 | |
| B. | 斜劈与小球组成的系统机械能不守恒 | |
| C. | 小球的机械能增加 | |
| D. | 斜劈的机械能增加 |
17.甲、乙两物体质量之比为m甲:m乙=5:1,甲从H高处自由下落,乙从2H高处同时自由下落,不计空气阻力,以下说法正确的是( )
| A. | 在下落过程中,同一时刻甲的速度比乙的速度大 | |
| B. | 在下落过程中,同一时刻甲的速度比乙的速度小 | |
| C. | 甲、乙在空气中运动的时间之比为1:2 | |
| D. | 甲落地时,乙距地面的高度为H |
4.障碍物宽度为10cm,下列各种波长中的波能出现最明显的衍射现象的波长是( )
| A. | 5cm | B. | 20cm | C. | 50cm | D. | 80cm |
14. 如图所示,一根轻弹簧下端固定,竖立在水平面上,其正上方A位置有一只小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零,小球下降阶段下列说法中正确的是( )
如图所示,一根轻弹簧下端固定,竖立在水平面上,其正上方A位置有一只小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零,小球下降阶段下列说法中正确的是( )
 如图所示,一根轻弹簧下端固定,竖立在水平面上,其正上方A位置有一只小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零,小球下降阶段下列说法中正确的是( )
如图所示,一根轻弹簧下端固定,竖立在水平面上,其正上方A位置有一只小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零,小球下降阶段下列说法中正确的是( )| A. | 在B位置小球加速度最大 | |
| B. | 在C位置小球速度最大 | |
| C. | 从A→C位置小球重力势能的减少量小于重力做的功 | |
| D. | 从A→D位置小球重力势能的减少等于弹簧弹性势能的增加 |
20.一弹簧振子做简谐运动,周期为T,下述正确的是( )
| A. | 若△t=$\frac{T}{2}$,则在t时刻和(t+△t)时刻弹簧长度一定相等 | |
| B. | 若t时刻和(t+△t)时刻振子运动速度大小相等,方向相反,则△t一定等于$\frac{T}{2}$的整数倍 | |
| C. | 若△t=T,则在t时刻和(t+△t)时刻振子运动的加速度一定相等 | |
| D. | 若t时刻和(t+△t)时刻振子运动位移的大小相等,方向相反,则△t一定等于T的整数倍 |

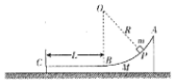 如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,在P点将一个质量m=0.2kg的物块(可视为质点)无初速度释放,物块滑至C点时恰好静止,已知物块与BC段的动摩擦因数μ=0.1,取重力加速度g=10m/s2,求:
如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,在P点将一个质量m=0.2kg的物块(可视为质点)无初速度释放,物块滑至C点时恰好静止,已知物块与BC段的动摩擦因数μ=0.1,取重力加速度g=10m/s2,求: 从受力特点来看,做简谐运动的物体所受到的回复力F=-kx,负号表示回复力F的方向始终与物体偏离平衡位置的位移x的方向相反,k为比例系数.相关文献表明,力学中的-切做简谐运动的物体,其往复运动的周期均可利用公式T=2π$\sqrt{\frac{m}{k}}$求解,m是做简谐运动的物体质量,k为回复力公式中的比例系数.
从受力特点来看,做简谐运动的物体所受到的回复力F=-kx,负号表示回复力F的方向始终与物体偏离平衡位置的位移x的方向相反,k为比例系数.相关文献表明,力学中的-切做简谐运动的物体,其往复运动的周期均可利用公式T=2π$\sqrt{\frac{m}{k}}$求解,m是做简谐运动的物体质量,k为回复力公式中的比例系数.