题目内容
10.如图,平行长直金属导轨水平放置,导轨间距为L,一端接有阻值为R的电阻,整个导轨处于竖直向下的匀强磁场中,磁感应强度大小为B.一根质量为m的金属杆置于导轨上,与导轨垂直并接触良好.己知金属杆在导轨上开始运动的初速度大小为V0,方向平行于导轨.忽略金属杆与导轨的电阻,不计摩擦.求金属杆运动到总路程的λ(0≤λ≤1)倍时,安培力的瞬时功率.
分析 金属棒运动切割磁感线产生感应电动势,回路中有感应电流,感应电流在磁场中受到安培力的作用,取极短的时间运用动量定理列式,运用微元法即可求得瞬时功率.
解答 解:设运动过程中任意时刻的速度为v,运动的总位移为x,则E=Blv,而i=$\frac{E}{R}$,则金属棒受到的安培力F=Bil=$\frac{{B}^{2}{l}^{2}v}{R}$
在极端的时间△t内,由动量定理得-F•△t=m•△v
即-$\frac{{B}^{2}{l}^{2}v△t}{R}$=m△v,对全过程累加得-$\frac{{B}^{2}{l}^{2}x}{R}$=mv0
当x'=λx时,v=v0-$\frac{{B}^{2}{l}^{2}λx}{mR}$,即v=(1-λ)v0
此时安培力F′=$\frac{(1-λ){B}^{2}{l}^{2}{v}_{0}}{R}$,瞬时功率P=F′v=$\frac{(1-λ)^{2}{B}^{2}{l}^{2}{v}_{0}^{2}}{R}$.
答:所以金属杆运动到总路程的λ(0≤λ≤1)倍时,安培力的瞬时功率为$\frac{(1-λ)^{2}{B}^{2}{l}^{2}{v}_{0}^{2}}{R}$.
点评 此题涉及微元法的应用,微元法在自主招生考试中经常出现,值得引起高度重视.同时,应用动量定理解决安培力的相关问题,在华约自主招生中经常出现,最近的是2011年华约自主招生物理试题第7题.

练习册系列答案
相关题目
14.理想实验是科学研究中的一种重要方法,它把可靠事实和理论思维结合起来,可以深刻地揭示自然规律.以下实验中属于理想实验的是( )
| A. | 验证平行四边形定则 | B. | 伽利略的斜面实验 | ||
| C. | 用DIS测物体的加速度 | D. | 利用自由落体运动测定反应时间 |
19.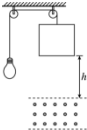 如图所示,一质量为m1=0.1kg的小灯泡通过双股柔软轻质导线与一质量为m2=0.3kg的正方形线框连接成闭合回路(图中用单股导线表示),已知线框匝数为N=10匝,总电阻为r=1Ω,线框正下方h=0.4m处有一水平方向的有界匀强磁场,磁感应强度为B=1T,磁场宽度与线框边长均为L=0.2m,忽略所有摩擦阻力及导线电阻,现由静止释放线框,当线框下边进入磁场的瞬间,加速度恰好为零,且小灯泡正常发光,g取10m/s2.则( )
如图所示,一质量为m1=0.1kg的小灯泡通过双股柔软轻质导线与一质量为m2=0.3kg的正方形线框连接成闭合回路(图中用单股导线表示),已知线框匝数为N=10匝,总电阻为r=1Ω,线框正下方h=0.4m处有一水平方向的有界匀强磁场,磁感应强度为B=1T,磁场宽度与线框边长均为L=0.2m,忽略所有摩擦阻力及导线电阻,现由静止释放线框,当线框下边进入磁场的瞬间,加速度恰好为零,且小灯泡正常发光,g取10m/s2.则( )
 如图所示,一质量为m1=0.1kg的小灯泡通过双股柔软轻质导线与一质量为m2=0.3kg的正方形线框连接成闭合回路(图中用单股导线表示),已知线框匝数为N=10匝,总电阻为r=1Ω,线框正下方h=0.4m处有一水平方向的有界匀强磁场,磁感应强度为B=1T,磁场宽度与线框边长均为L=0.2m,忽略所有摩擦阻力及导线电阻,现由静止释放线框,当线框下边进入磁场的瞬间,加速度恰好为零,且小灯泡正常发光,g取10m/s2.则( )
如图所示,一质量为m1=0.1kg的小灯泡通过双股柔软轻质导线与一质量为m2=0.3kg的正方形线框连接成闭合回路(图中用单股导线表示),已知线框匝数为N=10匝,总电阻为r=1Ω,线框正下方h=0.4m处有一水平方向的有界匀强磁场,磁感应强度为B=1T,磁场宽度与线框边长均为L=0.2m,忽略所有摩擦阻力及导线电阻,现由静止释放线框,当线框下边进入磁场的瞬间,加速度恰好为零,且小灯泡正常发光,g取10m/s2.则( )| A. | 小灯泡的电阻R=3Ω | |
| B. | 线框下边进入磁场的瞬间,小灯泡的速度v=3m/s | |
| C. | 在线框进入磁场区域的过程中,通过小灯泡的电荷量q=0.2C | |
| D. | 在线框穿过磁场区域的过程中,小灯泡消耗的电能ER=0.8J |
20. 如图所示,足够长的两平行金属板正对着竖直放置,它们通过导线与电源E、定值电阻R、开关S相连.闭合开关后,与两极板上边缘等高处有两个带负电小球A和B,它们均从两极板正中央由静止开始释放,两小球最终均打在极板上,(不考虑小球间的相互作用及对电场的影响)下列说法中正确的是( )
如图所示,足够长的两平行金属板正对着竖直放置,它们通过导线与电源E、定值电阻R、开关S相连.闭合开关后,与两极板上边缘等高处有两个带负电小球A和B,它们均从两极板正中央由静止开始释放,两小球最终均打在极板上,(不考虑小球间的相互作用及对电场的影响)下列说法中正确的是( )
 如图所示,足够长的两平行金属板正对着竖直放置,它们通过导线与电源E、定值电阻R、开关S相连.闭合开关后,与两极板上边缘等高处有两个带负电小球A和B,它们均从两极板正中央由静止开始释放,两小球最终均打在极板上,(不考虑小球间的相互作用及对电场的影响)下列说法中正确的是( )
如图所示,足够长的两平行金属板正对着竖直放置,它们通过导线与电源E、定值电阻R、开关S相连.闭合开关后,与两极板上边缘等高处有两个带负电小球A和B,它们均从两极板正中央由静止开始释放,两小球最终均打在极板上,(不考虑小球间的相互作用及对电场的影响)下列说法中正确的是( )| A. | 两小球在两板间运动的轨迹都是一条抛物线 | |
| B. | 两板间电压越大,小球在板间运动的时间越短 | |
| C. | 它们的运动时间一定相同 | |
| D. | 若两者的比荷相同,它们的运动轨迹可能相同 |
 如图所示,先后两次将同一个矩形线圈由匀强磁场中拉出,两次拉动的速度相同.第一次线圈长边与磁场边界平行,将线圈全部拉出磁场区,通过线圈的电流为I1,拉力做功W1、通过导线截面的电荷量为q1,第二次线圈短边与磁场边界平行,将线圈全部拉出磁场区域,通过线圈的电流为I2,拉力做功为W2、通过导线截面的电荷量为q2,则I1>I2,W1>W2,q1=q2.(三空均选填“>”、“=”或“<”)
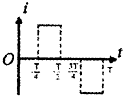
如图所示,先后两次将同一个矩形线圈由匀强磁场中拉出,两次拉动的速度相同.第一次线圈长边与磁场边界平行,将线圈全部拉出磁场区,通过线圈的电流为I1,拉力做功W1、通过导线截面的电荷量为q1,第二次线圈短边与磁场边界平行,将线圈全部拉出磁场区域,通过线圈的电流为I2,拉力做功为W2、通过导线截面的电荷量为q2,则I1>I2,W1>W2,q1=q2.(三空均选填“>”、“=”或“<”) 如图中的虚线上方空间有垂直线框平面的匀强磁场,直角扇形导线框绕垂直于线框平面的轴O以角速度ω匀速转动.设线框中感应电流方向以逆时针为正方向,那么在图中能正确描述线框从图所示位置开始转动一周的过程中,线框内感应电流随时间变化情况的是( )
如图中的虚线上方空间有垂直线框平面的匀强磁场,直角扇形导线框绕垂直于线框平面的轴O以角速度ω匀速转动.设线框中感应电流方向以逆时针为正方向,那么在图中能正确描述线框从图所示位置开始转动一周的过程中,线框内感应电流随时间变化情况的是( )


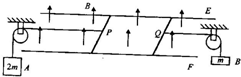 水平放置的两根足够长的平行金属导轨E、F间距L=2m,电阻忽略不计,处于磁感应强度大小B=1T竖直向上的匀强磁场中,质量均为m=0.8kg、电阻均为r=1Ω的P、Q两金属棒垂直导轨放置,导轨与金属棒之间的动摩擦因数为μ=0.5,且两者接触良好.P、Q分别通过光滑的定滑轮用足够长的轻绳连接质量为2m与m的两物体A、B,轻绳的一端分别水平垂直连接P、Q.开始时固定住两物体A、B,轻绳拉直但不张紧,整个装置处于静止状态,设最大静摩擦力等于滑动摩擦力,其中g取10m/s2.
水平放置的两根足够长的平行金属导轨E、F间距L=2m,电阻忽略不计,处于磁感应强度大小B=1T竖直向上的匀强磁场中,质量均为m=0.8kg、电阻均为r=1Ω的P、Q两金属棒垂直导轨放置,导轨与金属棒之间的动摩擦因数为μ=0.5,且两者接触良好.P、Q分别通过光滑的定滑轮用足够长的轻绳连接质量为2m与m的两物体A、B,轻绳的一端分别水平垂直连接P、Q.开始时固定住两物体A、B,轻绳拉直但不张紧,整个装置处于静止状态,设最大静摩擦力等于滑动摩擦力,其中g取10m/s2. 如图所示,金属杆MN在竖直平面内贴着光滑平行金属导轨下滑,导轨的间距l=10cm,导轨上端接有R=0.4Ω的电阻,金属杆MN的电阻r=0.1Ω,导轨电阻不计,整个装置处于B=0.5T的水平匀强磁场中,磁场方向垂直于导轨平面.当金属杆MN下滑时,不计空气阻力.求
如图所示,金属杆MN在竖直平面内贴着光滑平行金属导轨下滑,导轨的间距l=10cm,导轨上端接有R=0.4Ω的电阻,金属杆MN的电阻r=0.1Ω,导轨电阻不计,整个装置处于B=0.5T的水平匀强磁场中,磁场方向垂直于导轨平面.当金属杆MN下滑时,不计空气阻力.求 如图所示,一矩形金属框,可动边AB长为0.10m,电阻为0.20Ω,CD边电阻为0.80Ω,导轨电阻不计,匀强磁场的磁感应强度为0.50T.当AB边以15m/s的速度向右移动时,求:(1)感应电动势的大小;
如图所示,一矩形金属框,可动边AB长为0.10m,电阻为0.20Ω,CD边电阻为0.80Ω,导轨电阻不计,匀强磁场的磁感应强度为0.50T.当AB边以15m/s的速度向右移动时,求:(1)感应电动势的大小;