题目内容
5.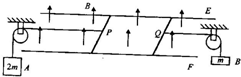 水平放置的两根足够长的平行金属导轨E、F间距L=2m,电阻忽略不计,处于磁感应强度大小B=1T竖直向上的匀强磁场中,质量均为m=0.8kg、电阻均为r=1Ω的P、Q两金属棒垂直导轨放置,导轨与金属棒之间的动摩擦因数为μ=0.5,且两者接触良好.P、Q分别通过光滑的定滑轮用足够长的轻绳连接质量为2m与m的两物体A、B,轻绳的一端分别水平垂直连接P、Q.开始时固定住两物体A、B,轻绳拉直但不张紧,整个装置处于静止状态,设最大静摩擦力等于滑动摩擦力,其中g取10m/s2.
水平放置的两根足够长的平行金属导轨E、F间距L=2m,电阻忽略不计,处于磁感应强度大小B=1T竖直向上的匀强磁场中,质量均为m=0.8kg、电阻均为r=1Ω的P、Q两金属棒垂直导轨放置,导轨与金属棒之间的动摩擦因数为μ=0.5,且两者接触良好.P、Q分别通过光滑的定滑轮用足够长的轻绳连接质量为2m与m的两物体A、B,轻绳的一端分别水平垂直连接P、Q.开始时固定住两物体A、B,轻绳拉直但不张紧,整个装置处于静止状态,设最大静摩擦力等于滑动摩擦力,其中g取10m/s2.(1)若始终固定住B,自由释放A,则A的最大速度是多少?
(2)若自由释放A,当A的速度至少为多大时再释放B,B才能下落?
(3)在(2)之后随着A速度增大,B能不能继续保持静止?
分析 (1)根据切割感应电动势,及闭合电路欧姆定律,及牛顿第二定律,再结合安培力表达式,即可求解;
(2)先确定Q受到摩擦力方向,再依据静摩擦力最大时,安培力最小,结合安培力表达式,即可求解最小速度.
(3)随着A速度增大,安培力增大,Q所受摩擦力先向左逐渐减小,当安培力等于8N时摩擦力为零,之后安培力增大,摩擦力方向为向右并逐渐增大,静摩擦力最大时,安培力有最大值,而此时A正好达最大速度做匀速运动,速度不会再增加,故B能继续保持静止
解答 解:(1)若始终固定住B,自由释放A,当A的运动速度为v时,P切割产生的电动势E=BLv
感应电流为$I=\frac{BLv}{2r}$
则P棒受到的安培力为$F=BIL=\frac{{B}_{\;}^{2}{L}_{\;}^{2}v}{2r}$
A向下做加速运动,$2mg-{F}_{T}^{\;}=2ma$
P向左做加速度大小相同的加速运动${F}_{T}^{\;}-μmg-\frac{{B}_{\;}^{2}{L}_{\;}^{2}v}{2r}=ma$
可得:$2mg-μmg-\frac{{B}_{\;}^{2}{L}_{\;}^{2}v}{2r}=3ma$
A向下(P向左)做加速度减小的加速运动,直至以最大速度做匀速运动
$2mg=\frac{{B}_{\;}^{2}{L}_{\;}^{2}{v}_{m}^{\;}}{2r}+μmg$
得${v}_{m}^{\;}=6m/s$
(2)要使Q保持不下滑,Q所受摩擦力的方向水平向左,则F+f=mg
静摩擦力最大时,安培力最小,最小值为Fmin=4N;
由F=BIL=$\frac{{B}_{\;}^{2}{L}_{\;}^{2}v}{2r}$,得对应的最小速度为vmin=2m/s
即当A速度为2m/s时释放B,B才不下落.
(3)随着A速度增大,安培力增大,Q所受摩擦力先向左逐渐减小,当安培力等于8N时摩擦力为零,之后安培力增大,摩擦力方向为向右并逐渐增大,F=mg+f
静摩擦力最大时,安培力有最大值${F}_{max}^{\;}=12N$
对应的最大速度${v}_{max}^{\;}=6m/s$
而此时A正好达最大速度做匀速运动,速度不会再增加,故B能继续保持静止.
答:(1)若始终固定住B,自由释放A,则A的最大速度是6m/s
(2)若自由释放A,当A的速度至少为2m/s时再释放B,B才能下落
(3)在(2)之后随着A速度增大,B能继续保持静止
点评 本题考查力电综合问题,掌握切割感应电动势的求解方法,理解牛顿第二定律的应用,注意第2问,依据静摩擦力最大时,来确定安培力最小,从而判定最小速度.

| A. | 若物体运动过程中速率不变,则动量变化量为零 | |
| B. | 物体的动量变化得越快,说明物体所受合外力越大 | |
| C. | 若外力对物体做功和为零,则物体的动能守恒 | |
| D. | 运动员接篮球时手臂有弯曲回收动作,其作用是减小篮球对手的冲量. |
 如图所示,两条平行虚线之间存在匀强磁场,磁场方向垂直纸面向里,虚线间的距离为l,金属圆环的直径也是l.圆环从左边界进入磁场,以垂直于磁场边界的恒定速度v穿过磁场区域.则下列说法正确的是( )
如图所示,两条平行虚线之间存在匀强磁场,磁场方向垂直纸面向里,虚线间的距离为l,金属圆环的直径也是l.圆环从左边界进入磁场,以垂直于磁场边界的恒定速度v穿过磁场区域.则下列说法正确的是( )| A. | 感应电流的大小先增大后减小 | |
| B. | 感应电流的方向先逆时针后顺时针 | |
| C. | 金属圆环受到的安培力先向左后向右 | |
| D. | 进入磁场时感应电动势平均值$\overline{E}$=$\frac{1}{2}$πBav |
 如图所示,两足够长的平行粗糙金属导轨MN,PQ相距L=1m.导轨平面与水平面夹角为α=30°.导轨电阻不计.磁感应强度B1=2T的匀强磁场垂直导轨平面向上,长L=1m的金属棒ab垂直于MN,PQ放置在导轨上,两者间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,金属棒的质量m1=2kg,电阻R1=lΩ,两金属棒导轨的上端连接右侧电路.电路和中通过导线接一对水平放置的平行金属板,两板间的距离和板长增为d=0.5m,定值电阻R2=3Ω,将金属棒由静止释放.重力加速度g取10m/s2,
如图所示,两足够长的平行粗糙金属导轨MN,PQ相距L=1m.导轨平面与水平面夹角为α=30°.导轨电阻不计.磁感应强度B1=2T的匀强磁场垂直导轨平面向上,长L=1m的金属棒ab垂直于MN,PQ放置在导轨上,两者间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,金属棒的质量m1=2kg,电阻R1=lΩ,两金属棒导轨的上端连接右侧电路.电路和中通过导线接一对水平放置的平行金属板,两板间的距离和板长增为d=0.5m,定值电阻R2=3Ω,将金属棒由静止释放.重力加速度g取10m/s2, 两个试管由一软管联通(如图所示),左边试管由一段长为24cm的水银柱封住一段长为60cm、温度为300K的气体,这时水银面距管侧面小孔还有16cm,右边空试管为防溢用.现有一控温系统可以持续升高或降低气体的温度,当气体温度升高到一定值时水银会从左边试管溢到右边的试管中.左边试管固定不动,右边的试管可以上下移动,上移时可使右边试管中的水银回流到左边试管、从而控制左边试管中水银柱的高度.
两个试管由一软管联通(如图所示),左边试管由一段长为24cm的水银柱封住一段长为60cm、温度为300K的气体,这时水银面距管侧面小孔还有16cm,右边空试管为防溢用.现有一控温系统可以持续升高或降低气体的温度,当气体温度升高到一定值时水银会从左边试管溢到右边的试管中.左边试管固定不动,右边的试管可以上下移动,上移时可使右边试管中的水银回流到左边试管、从而控制左边试管中水银柱的高度.
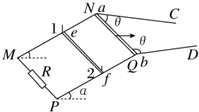 如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ.均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止.空间有方向竖直的匀强磁场(图中未画出).两金属棒与导轨保持良好接触.不计所有导轨和ab棒的电阻,ef棒的阻值为R,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g.
如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ.均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止.空间有方向竖直的匀强磁场(图中未画出).两金属棒与导轨保持良好接触.不计所有导轨和ab棒的电阻,ef棒的阻值为R,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g. 如图所示,EFGH为边长为L的正方形金属线框,线框对角线EG和y轴重合、顶点E位于坐标原点O处.在y轴右侧的第I象限一定范围内有一垂直纸面向里的匀强磁场,磁场下边界与x轴重合,上边界为直线0A且与线框的EH边重合.从t=0时刻起,线圈以恒定的速度v沿垂直于磁场上边界0A的方向穿过磁场区域.取线框中感应电流沿逆时针方向为正,则在线圈穿越磁场区域的过程中,感应电流i随时间/变化的图线是图乙中的( )
如图所示,EFGH为边长为L的正方形金属线框,线框对角线EG和y轴重合、顶点E位于坐标原点O处.在y轴右侧的第I象限一定范围内有一垂直纸面向里的匀强磁场,磁场下边界与x轴重合,上边界为直线0A且与线框的EH边重合.从t=0时刻起,线圈以恒定的速度v沿垂直于磁场上边界0A的方向穿过磁场区域.取线框中感应电流沿逆时针方向为正,则在线圈穿越磁场区域的过程中,感应电流i随时间/变化的图线是图乙中的( )



 在光滑水平面上向右运动的物体受力情况如图所示.g取10m/s2,请根据图中的数据求:
在光滑水平面上向右运动的物体受力情况如图所示.g取10m/s2,请根据图中的数据求: