题目内容
5.“探路者”号宇宙飞船在宇宙深处飞行过程中,发现A、B两颗天体各有一颗靠近表面飞行的卫星,并测得两颗卫星的周期相等,以下判断正确的是( )| A. | 天体A、B的密度不同 | |
| B. | 天体A、B的质量一定相等 | |
| C. | 两颗卫星的线速度一定相等 | |
| D. | 天体A、B表面的重力加速度与它们的半径成正比 |
分析 卫星绕球形天体运动时,由万有引力提供向心力,根据牛顿第二定律和万有引力定律得出天体的质量与卫星周期的关系式,再得出天体密度与周期的关系式,然后进行比较.
解答 解:对近地卫星有$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$,卫星是环绕天体质量被约掉,$M=\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{G{T}_{\;}^{2}}$,因为天体A、B的半径不一定相等,所以天体A、B的质量不一定相等,故B错误;
根据$v=\frac{2πR}{T}$,周期相同,但半径不一定相同,所以线速度不一定相等,故C错误;
根据$ρ=\frac{M}{V}=\frac{\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{G{T}_{\;}^{2}}}{\frac{4π{R}_{\;}^{3}}{3}}=\frac{3π}{G{T}_{\;}^{2}}$,可知天体A、B的密度一定相等,故A错误;
根据$mg=G\frac{Mm}{{R}_{\;}^{2}}$得$g=G\frac{M}{{R}_{\;}^{2}}=\frac{4{π}_{\;}^{2}R}{{T}_{\;}^{2}}$∝R,故D正确
故选:D
点评 本题是卫星绕行星运动的问题,要建立好物理模型,采用比例法求解.要熟练应用万有引力定律、圆周运动的规律结合处理这类问题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
15.A和B两行星绕同一恒星C做圆周运动,旋转方向相同,A行星的周期为T,B行星的周期为5T,从某一时刻两行星相距最近开始,则( )
| A. | 经过5T两行星相距最近 | B. | 经过$\frac{3}{2}$T两行星相距最近 | ||
| C. | 经过$\frac{15}{8}$T两行星相距最远 | D. | 经过$\frac{7}{8}$T两行星相距最远 |
13.甲星球绕乙星球做圆周运动的半径为r1,周期为T1;丙星球绕甲星球做圆周运动的半径为r2,周期为T2.引力常量为G,不计周围其他天体的影响,则根据给定条件( )
| A. | 能得到表达式$\frac{{{r}_{1}}^{3}}{{{T}_{1}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{T}_{2}}^{2}}$ | |
| B. | 能求出甲星球的质量 | |
| C. | 能求出甲星球与乙星球之间的万有引力 | |
| D. | 能求出甲星球与丙星球之间的万有引力 |
20.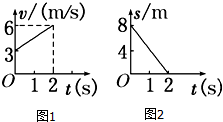 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
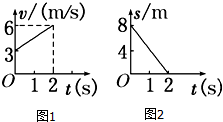 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )| A. | 质点的初速度为3 m/s | |
| B. | 2s末质点速度大小为6 m/s | |
| C. | 质点做曲线运动的加速度为1.5m/s2 | |
| D. | 质点初速度的方向与合外力方向垂直 |
10.下列数据中,可以算出氢气密度的是( )
| A. | 氢气的摩尔质量和阿伏伽德罗常数 | B. | 氢气分子的体积和阿伏伽德罗常数 | ||
| C. | 氢气的摩尔质量和氢气的摩尔体积 | D. | 氢气分子的质量和氢气分子的体积 |
17.关于黑体及黑体辐射下列说法正确的是( )
| A. | 黑体是真实存在的 | |
| B. | 黑体辐射电磁波的强度与温度有关 | |
| C. | 随着温度升高黑体辐射中的有些成分会增强,有些成分会减弱 | |
| D. | 随着温度升高黑体辐射中强度最强的那一部分始终不变 |